 por Claudin » Seg Jul 25, 2011 03:52
por Claudin » Seg Jul 25, 2011 03:52
Como por exemplo aos 4:45 no vídeo 26 em que:
1º ex:

Gostaria de saber detalhadamente como calcular para obter este valor.
2º exemplo que gostaria de deixar, seria o

O resultado só é

porque representa metade da área da figura geométrica plana?
Gostaria de uma explicação detalhada de como fazer os devidos cálculos para resolução dos seguintes exercícios.
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por m0x0 » Seg Jul 25, 2011 07:13
por m0x0 » Seg Jul 25, 2011 07:13
Para o 1º exemplo tens:
![\int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3} \int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}](/latexrender/pictures/538921db209f46819ed52cb1e50d45e1.png)
Para o 2º exemplo tens:
![\int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2} \int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}](/latexrender/pictures/cc6079b75c307df14664092f82fceb77.png)
Espero ter ajudado.
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Jul 25, 2011 09:07
por LuizAquino » Seg Jul 25, 2011 09:07
Claudin escreveu:Como calcular uma integral?
Como foi feito nestas vídeo-aulas, podemos calcular a integral definida utilizando a sua definição, isto é, basicamente através de um limite da Soma de Riemman.
Nas próximas vídeo-aulas será apresentado um teorema muito importante (o Teorema Fundamental do Cálculo) que nos permite calcular uma integral definida de uma maneira mais simples do que através de sua definição.
Claudin escreveu:Como por exemplo aos 4:45 no vídeo 26 em que:
1º ex:

O cálculo dessa integral é justificado devido ao que foi exposto na vídeo-aula "25. Cálculo I - Área de Superfícies Planas".
Claudin escreveu:2º exemplo que gostaria de deixar, seria o

O resultado só é

porque representa metade da área da figura geométrica plana?
No vídeo "26. Cálculo I - Integral Definida" é apresentado a
definição de integral definida e é exibido como calcular essa integral pela
definição.
Além disso, foi exposto no vídeo que se f(x) é uma função contínua e positiva no intervalo [a, b], então

representa a área entre o gráfico da função e o eixo x no intervalo [a, b].
Acontece que a área entre o gráfico da reta f(x) = x e o eixo x no intervalo [0, 1] é um triângulo de base e altura iguais a 1. Essa é uma interpretação geométrica para
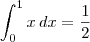
.
Editado pela última vez por
LuizAquino em Seg Jul 25, 2011 09:37, em um total de 3 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LuizAquino » Seg Jul 25, 2011 09:10
por LuizAquino » Seg Jul 25, 2011 09:10
m0x0 escreveu:Para o 1º exemplo tens:
![\int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3} \int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}](/latexrender/pictures/538921db209f46819ed52cb1e50d45e1.png)
Para o 2º exemplo tens:
![\int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2} \int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}](/latexrender/pictures/cc6079b75c307df14664092f82fceb77.png)
Espero ter ajudado.
Note que:
![\int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx \int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx](/latexrender/pictures/863cd990b2915099d513cd20af2fefe3.png)
![\int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx \int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx](/latexrender/pictures/dfc0fdd836390fa915ac492ad7604d4a.png)
O que temos é:
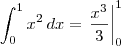
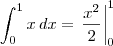
Cuidado com as notações!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Seg Jul 25, 2011 13:41
por Claudin » Seg Jul 25, 2011 13:41
LuizAquino escreveu:Note que:
![\int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx \int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx](/latexrender/pictures/863cd990b2915099d513cd20af2fefe3.png)
![\int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx \int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx](/latexrender/pictures/dfc0fdd836390fa915ac492ad7604d4a.png)
O que temos é:
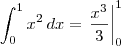
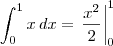
Cuidado com as notações!
Não consegui compreender como chegar em:
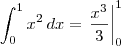
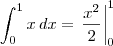
se o que temos a início seria:

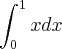
Gostaria de saber detalhadamente como obter o cálculo da integral.
Obrigado Luiz e mOxO
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Seg Jul 25, 2011 15:01
por Molina » Seg Jul 25, 2011 15:01
Boa tarde, Claudin.
Claudin escreveu:LuizAquino escreveu:Note que:
![\int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx \int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx](/latexrender/pictures/863cd990b2915099d513cd20af2fefe3.png)
![\int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx \int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx](/latexrender/pictures/dfc0fdd836390fa915ac492ad7604d4a.png)
O que temos é:
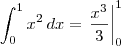
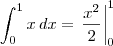
Cuidado com as notações!
Não consegui compreender como chegar em:
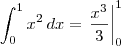
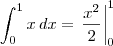
se o que temos a início seria:

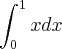
Gostaria de saber detalhadamente como obter o cálculo da integral.
Obrigado Luiz e mOxO
Se me permite tentar explicar, você verá mais a frente que a integral está para a derivada, assim como a soma está para subtração e a multiplicação está para a divisão. Ou seja, são operações opostas.
Quando você tem a integral de uma função f(x), dentre outras coisas, você está interessado em saber qual a derivada que resulta em f(x).
Por exemplo:

Você está interessado em achar qual a função que quando eu derivar vai resultar em

.
Como já foi exposto acima, existem algumas técnicas e definições que facilitam em muitos cálculos.
Perceba que o resultado que te apresentaram de

é

.
Agora derive

e perceba que você vai encontrar

.
Há ainda algumas definições como integral definida e indefinida que não vou entrar em detalhes ainda.
Compare agora o que eu disse com o seu outro exemplo de integral.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Seg Jul 25, 2011 19:40
por Claudin » Seg Jul 25, 2011 19:40
Consegui compreender o que você disse Molina.
Sendo:

Derivando

O que seria diferente de derivar a expressão toda.
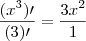
Correto?
Editado pela última vez por
Claudin em Seg Jul 25, 2011 19:48, em um total de 1 vez.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Seg Jul 25, 2011 19:48
por Claudin » Seg Jul 25, 2011 19:48
Sendo:
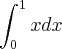
Derivando:
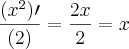
O que seria diferente de derivar a expressão toda:

Correto?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Seg Jul 25, 2011 20:09
por Molina » Seg Jul 25, 2011 20:09
Boa noite, Claudin.
Você precisa derivar TODA A FUNÇÃO e não só o numerador.
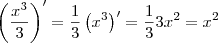


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Ter Jul 26, 2011 00:56
por Claudin » Ter Jul 26, 2011 00:56
Boa Noite Molina,
Agora sim compreendi.
Mas como chegar em

e

Gostaria de saber qual próximo passo para ajudar a resolver uma integral.
Obrigado por ajudar a esclarecer a dúvida.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Ter Jul 26, 2011 01:14
por Molina » Ter Jul 26, 2011 01:14
Boa noite.
Claudin escreveu:Boa Noite Molina,
Agora sim compreendi.
Mas como chegar em

e

Gostaria de saber qual próximo passo para ajudar a resolver uma integral.
Obrigado por ajudar a esclarecer a dúvida.

Assim como na derivada, a integral possui alguma funções que podem ser generalizadas, sem precisar fazer muita conta. Para esses seus exemplos, temos que:
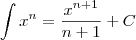
onde C é uma constante e sempre aparecerá em integrais indefinidas (quando não aparece os limites da integral); e
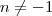
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Ter Jul 26, 2011 01:18
por Claudin » Ter Jul 26, 2011 01:18
m0x0 escreveu:Para o 1º exemplo tens:
![\int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3} \int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}](/latexrender/pictures/538921db209f46819ed52cb1e50d45e1.png)
Para o 2º exemplo tens:
![\int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2} \int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}](/latexrender/pictures/cc6079b75c307df14664092f82fceb77.png)
Espero ter ajudado.
Como por exemplo neste caso, ele substituiu os valores 0 e 1, no caso.
Aí encontrou direto os resultados
Mas não compreendo como ele chegou em

e

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Ter Jul 26, 2011 09:46
por LuizAquino » Ter Jul 26, 2011 09:46
Claudin,
Considerando as suas postagens, ao que parece você estudou a introdução sobre integrais definidas, mas você não estudou além da introdução.
Depois dessa primeira parte que apresenta a integral definida como o limite de uma Soma de Riemann, os livros de Cálculo geralmente apresentam o Teorema Fundamental do Cálculo.
Nesse contexto, é interessante que você primeiro estude essa parte do conteúdo para depois tirar as suas dúvidas.
É importante destacar também que antes de estudar o Teorema Fundamental do Cálculo é interessante revisar o conceito de antiderivada (ou primitiva) de uma função.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Ter Jul 26, 2011 12:36
por Claudin » Ter Jul 26, 2011 12:36
Correto Luiz, Vou seguir sua dica.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4579 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2865 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 porque representa metade da área da figura geométrica plana?
porque representa metade da área da figura geométrica plana?
![\int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3} \int_{0}^{1}x^2dx=\int_{0}^{1}[\frac{x^3}{3}]=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}](/latexrender/pictures/538921db209f46819ed52cb1e50d45e1.png)
![\int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2} \int_{0}^{1}xdx=\int_{0}^{1}[\frac{x^2}{2}]=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}](/latexrender/pictures/cc6079b75c307df14664092f82fceb77.png)

porque representa metade da área da figura geométrica plana?
 representa a área entre o gráfico da função e o eixo x no intervalo [a, b].
representa a área entre o gráfico da função e o eixo x no intervalo [a, b].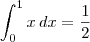 .
.
![\int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx \int_{0}^{1}x^2\,dx\neq \int_{0}^{1}[\frac{x^3}{3}]\,dx](/latexrender/pictures/863cd990b2915099d513cd20af2fefe3.png)
![\int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx \int_{0}^{1}x\,dx \neq \int_{0}^{1}[\frac{x^2}{2}]\,dx](/latexrender/pictures/dfc0fdd836390fa915ac492ad7604d4a.png)
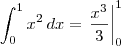
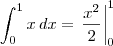

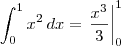
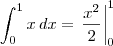

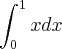


 .
. é
é  .
. e perceba que você vai encontrar
e perceba que você vai encontrar  .
.



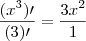

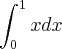
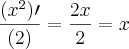


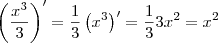



 e
e 


e
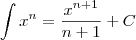
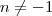

 e
e 


