 por Claudin » Ter Jul 19, 2011 19:49
por Claudin » Ter Jul 19, 2011 19:49
![\lim_{x\rightarrow4}\frac{\sqrt[]{x}-2}{x-4} \lim_{x\rightarrow4}\frac{\sqrt[]{x}-2}{x-4}](/latexrender/pictures/d362f6924163d5e222ada12442c0683e.png)
Talvez estou errando nos cálculos. Mas sem utilizar L'Hospital, utilizando métodos algébricos eu só cheguei em indeterminação

.
Cheguei a multiplicar o numerador e o denominador por

e encontrei

Depois tentei multiplicando o numerador e o numerador por
![\sqrt[]{x}+2 \sqrt[]{x}+2](/latexrender/pictures/e7d475d5cd1bb6d15ae38a4043177604.png)
e encontrei

Alguém explica este exercício?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Jul 19, 2011 21:02
por FilipeCaceres » Ter Jul 19, 2011 21:02
Olá Claudin,
Observe que

Agora tente resolver, caso tenha dificuldades, poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Qua Jul 20, 2011 00:23
por Claudin » Qua Jul 20, 2011 00:23
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jul 20, 2011 00:23
por Claudin » Qua Jul 20, 2011 00:23
Só pra constar, ajudas desse modo são muito mais construtivas Filipe
Muito obrigado.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Jul 20, 2011 09:23
por LuizAquino » Qua Jul 20, 2011 09:23
Claudin escreveu:Só pra constar, ajudas desse modo são muito mais construtivas Filipe
E note que ele
não resolveu o exercício! Ele apenas lhe deu uma
dica para você mesmo conseguir fazer (o que é muito melhor para o seu aprendizado).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qua Jul 20, 2011 09:24
por giulioaltoe » Qua Jul 20, 2011 09:24
voce também poderia fazer por mudança de variaveis! colocando
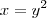
assim o y ia tender 2
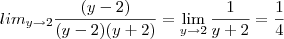
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por Claudin » Qua Jul 20, 2011 11:12
por Claudin » Qua Jul 20, 2011 11:12
Mas foi uma dica, em que, utilizou a teoria e parte da prática, não foi uma dica "seca". E foi muito proveitoso para meus estudos.
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Jul 20, 2011 11:31
por LuizAquino » Qua Jul 20, 2011 11:31
Claudin escreveu:Mas foi uma dica, em que, utilizou a teoria e parte da prática, não foi uma dica "seca". E foi muito proveitoso para meus estudos.
Apenas por curiosidade, na sua opinião, qual é a diferença entre essa dica e a que foi dada, por exemplo, no tópico abaixo?
Re: Limiteviewtopic.php?f=120&t=5290&#p17976
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Jul 20, 2011 11:33
por Claudin » Qua Jul 20, 2011 11:33
São equivalentes.

Mas em alguns casos mais complexos nem com a dica o aluno que possui a dúvida chega ao resultado e quando retorna ao tópico ele recebe mais dicas, em vez da solução para ajudar nos estudos.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6639 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4785 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5112 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7249 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4427 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow4}\frac{\sqrt[]{x}-2}{x-4} \lim_{x\rightarrow4}\frac{\sqrt[]{x}-2}{x-4}](/latexrender/pictures/d362f6924163d5e222ada12442c0683e.png)
 .
. e encontrei
e encontrei 
![\sqrt[]{x}+2 \sqrt[]{x}+2](/latexrender/pictures/e7d475d5cd1bb6d15ae38a4043177604.png) e encontrei
e encontrei 



![\lim_{x\rightarrow4}\frac{\sqrt[]{x}-2}{x-4}. \frac{\sqrt[]{x}+2}{\sqrt[]{x}+2} \lim_{x\rightarrow4}\frac{\sqrt[]{x}-2}{x-4}. \frac{\sqrt[]{x}+2}{\sqrt[]{x}+2}](/latexrender/pictures/2cf2dcc29191235ed9e631c8e584fd7e.png)
![\lim_{x\rightarrow4}\frac{1}{\sqrt[]{x}+2}\Rightarrow \frac{1}{\sqrt[]{4}+2}= \frac{1}{4} \lim_{x\rightarrow4}\frac{1}{\sqrt[]{x}+2}\Rightarrow \frac{1}{\sqrt[]{4}+2}= \frac{1}{4}](/latexrender/pictures/4e56b85bf2a34ba7026f0586f440489f.png)


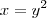 assim o y ia tender 2
assim o y ia tender 2 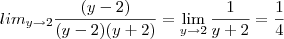

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
