
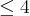 , tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo.
, tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo.Respondi assim:
volume desse sólido é dado por dV = A.dz, já que altura se expande no eixo Oz. A seção transversal do volume possui raio variável, tal que
 , sendo p o raio.
, sendo p o raio.Com a observação: "tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo", tem se, um duplo cone (acima e abaixo da origem no eixo Oz), só que partido ao meio na linha do eixo Ox.
A área então do círculo partido será pi.p², (repetindo, p é o raio variável), então:
E agora me perdi...Socorro!


 , tal que cada uma de suas seções transversais perpendiculares ao eixo Ox é um semicírculo.
, tal que cada uma de suas seções transversais perpendiculares ao eixo Ox é um semicírculo.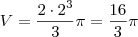 . Vamos confirmar isso aplicando integrais.
. Vamos confirmar isso aplicando integrais. .
.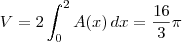


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.