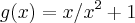
(i) Determine os pontos do gráfico de g em que as retas tangentes, nestes pontos, sejam
paralelas ao eixo x.
(ii) Estude o sinal de g(x).
(iii) Calcule:
g(x)

e g(x)
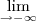
(iv) Utilizando as informações acima, faça um esboço do gráfico de g.

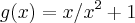

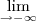

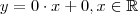 ) possuem o coeficiente angular nulo . São retas descritas por equações como por exemplo
) possuem o coeficiente angular nulo . São retas descritas por equações como por exemplo  ;
; 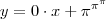 onde x varia-se livremente nos conjunto dos reais .
onde x varia-se livremente nos conjunto dos reais . ,
,  e
e 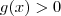 , para que números reais cada caso acontecerá ??
, para que números reais cada caso acontecerá ??  no infinito corresponde a estudar a tendência entre a razão do termo dominante presente do numerador de g(x) pelo termo dominante presente no denominador desta aplicação .
no infinito corresponde a estudar a tendência entre a razão do termo dominante presente do numerador de g(x) pelo termo dominante presente no denominador desta aplicação .  .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)