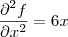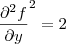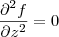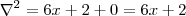[Gradiente - Cálculo 3] Dúvida exercício

por **ferfer** » Seg Ago 05, 2013 15:54

Boa tarde galera,
Então, minha dúvida é sobre gradiente do exercício em negrito abaixo:

Considere a função f = x cos(y) + y cos(z) + z cos(x). Calcule ?²f , onde ?² = ? . (?f)

Então, cálculo o gradiente (dF1/dx, dF2/dy, dF3/dz) e depois?
Valeu, obrigado

por **Russman** » Seg Ago 05, 2013 16:33

O operador Laplaciano é indicado por $\bigtriangledown ^2$ e ele calcula a divergência de um campo gradiente! Isto é,

$\bigtriangledown ^2 = \bigtriangledown \cdot \bigtriangledown = \frac{\mathrm{d^2} }{\mathrm{d} x^2} + \frac{\mathrm{d^2} }{\mathrm{d} y^2} + \frac{\mathrm{d^2} }{\mathrm{d} z^2}$

pois definimos o operador nabla como

$\bigtriangledown =\frac{\mathrm{d} }{\mathrm{d} x}\widehat{i}+ \frac{\mathrm{d} }{\mathrm{d} y}\widehat{j}+ \frac{\mathrm{d} }{\mathrm{d} z}\widehat{k}$ .

Portando, basta você derivar o campo escalar

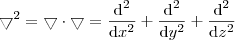
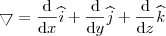duas vezes para

,

e

que você terá calculado o Laplaciano.

Exemplo: f=x^3 + y^2 + z

$\bigtriangledown ^2f= \left (\frac{\mathrm{d^2} }{\mathrm{d} x^2} + \frac{\mathrm{d^2} }{\mathrm{d} y^2} + \frac{\mathrm{d^2} }{\mathrm{d} z^2} \right )f =\left ( \frac{\mathrm{d^2} }{\mathrm{d} x^2} + \frac{\mathrm{d^2}}{\mathrm{d} y^2} + \frac{\mathrm{d^2} }{\mathrm{d} z^2} \right )\left ( x^3 + y^2 + z \right ) = 6x +2$

por **ferfer** » Seg Ago 05, 2013 16:39

Desculpa, mas não entendi, estou começando a ver cálculo 3!
Poderia dar um exemplo com resolução? Pode criar uma outra função, a fim que eu não quero a resposta, desejo realizar o exemplo que postei.
Obrigado

por **temujin** » Seg Ago 05, 2013 20:54

Foi exatamente isto que o Russman fez.

tome por exemplo a função:

f = x^3+y^2+z

O gradiente de f é o vetor que contém as derivadas parciais de f:

$\frac{\partial f}{\partial x} = 3x^2$
$\frac{\partial f}{\partial y} = 2y$
$\frac{\partial f}{\partial z} = 1$

Logo, o gradiente de f é dado por:

$\nabla = (3x^2 ; 2y ; z)$

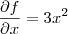
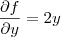
Como ele mostrou, para obter o laplaciano, $\nabla^2$ , basta derivar novamente:

$\frac{\partial^2 f}{\partial x^2} = 6x$
$\frac{\partial^2 f}{\partial y}^2 = 2$
$\frac{\partial^2 f}{\partial z^2} = 0$

Logo, $\nabla^2 = 6x+2+0 = 6x+2$

Faça o mesmo com a sua função. Basta somar as segundas derivadas parciais.

[Gradiente - Cálculo 3] Dúvida exercício

[Gradiente - Cálculo 3] Dúvida exercício

[Gradiente - Cálculo 3] Dúvida exercício

Re: [Gradiente - Cálculo 3] Dúvida exercício

Re: [Gradiente - Cálculo 3] Dúvida exercício

Re: [Gradiente - Cálculo 3] Dúvida exercício

Quem está online