 por Silva339 » Ter Mai 07, 2013 18:02
por Silva339 » Ter Mai 07, 2013 18:02
O potencial elétrico do ponto (x,y) e dado por
![v=\frac{4}{\sqrt[]{16-x^2-y^2}} v=\frac{4}{\sqrt[]{16-x^2-y^2}}](/latexrender/pictures/c1a1028d9fc8ea8fb02bab5030beecac.png)
( v em volts) determine e represente o xy as curvas equipotenciais pra 2V e 3V
como fazer essa questão ??????
-
Silva339
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Ter Mar 19, 2013 22:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Ter Mai 07, 2013 23:40
por young_jedi » Ter Mai 07, 2013 23:40
substitua o v da expressão pelos potenciais 2 e 3 V e encontre uma relação entre x e y
provavelmente você vai obter uma circunferência pra cada caso com raios direntes
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Silva339 » Ter Mai 07, 2013 23:54
por Silva339 » Ter Mai 07, 2013 23:54
já tentei varias vezes não da certo...
-
Silva339
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Ter Mar 19, 2013 22:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Qua Mai 08, 2013 00:00
por young_jedi » Qua Mai 08, 2013 00:00
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Silva339 » Qua Mai 08, 2013 00:49
por Silva339 » Qua Mai 08, 2013 00:49
Vc substitui o V= 2 e elevou ao quadrado ?
E por que deu 16 ?? vc fez 4^2 = 16 ??
é o x^3 como vc achou???
-
Silva339
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Ter Mar 19, 2013 22:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Qua Mai 08, 2013 21:39
por young_jedi » Qua Mai 08, 2013 21:39
o x ao cubo foi erro de digitação meu desculpe é x ao quardrado, e oque eu fiz foi elevar toda a equação ao quadrado
e substituir o v=2, e o 16 é realmente 4 ao quadrado
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (pêndulo-física)alguém ajuda achar energia potencial ?
por gustavoluiss » Ter Set 06, 2011 15:17
- 6 Respostas
- 3957 Exibições
- Última mensagem por gustavoluiss

Qua Set 07, 2011 01:55
Álgebra Elementar
-
- Circuito Elétrico
 por Rafael16 » Seg Mar 18, 2013 19:19
por Rafael16 » Seg Mar 18, 2013 19:19
- 1 Respostas
- 11757 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:43
Eletricidade I
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15142 Exibições
- Última mensagem por gutorocher

Sex Jul 23, 2010 13:04
Geometria Analítica
-
- Circuito Elétrico sem solução.
 por Sobreira » Qui Set 19, 2013 02:20
por Sobreira » Qui Set 19, 2013 02:20
- 3 Respostas
- 7920 Exibições
- Última mensagem por young_jedi

Sáb Set 21, 2013 11:27
Aritmética
-
- Campo elétrico resultante, socorro!!
por Lenin » Ter Mai 07, 2013 23:57
- 0 Respostas
- 2328 Exibições
- Última mensagem por Lenin

Ter Mai 07, 2013 23:57
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![v=\frac{4}{\sqrt[]{16-x^2-y^2}} v=\frac{4}{\sqrt[]{16-x^2-y^2}}](/latexrender/pictures/c1a1028d9fc8ea8fb02bab5030beecac.png) ( v em volts) determine e represente o xy as curvas equipotenciais pra 2V e 3V
( v em volts) determine e represente o xy as curvas equipotenciais pra 2V e 3V
![v=\frac{4}{\sqrt[]{16-x^2-y^2}} v=\frac{4}{\sqrt[]{16-x^2-y^2}}](/latexrender/pictures/c1a1028d9fc8ea8fb02bab5030beecac.png) ( v em volts) determine e represente o xy as curvas equipotenciais pra 2V e 3V
( v em volts) determine e represente o xy as curvas equipotenciais pra 2V e 3V



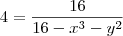


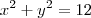




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)