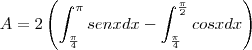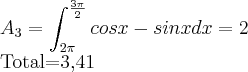por Deivid » Qui Set 23, 2010 16:25
por Deivid » Qui Set 23, 2010 16:25
Olá novamente comunidade AjudaMatematica, preciso da ajuda de vocês.
Tenho a seguinte questão:"Use a fórmula

para calcular a integral
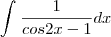
"
Eu não estou conseguindo resolver, nunca resolvi nenhuma com sen².
A outra duvida é na seguinte questão: "Calcular a área da região delimitada por

e

,

e

.Apresente o gráfico da região desenvolvido em um software gráfico."
O Grafico:

Resultados que obtive:

Porem, área até onde sei tem que ser diferente de 0, alguém pode me explicar o que ha de errado?
Obrigado, Deivid Steffens.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Neperiano » Qui Set 23, 2010 17:36
por Neperiano » Qui Set 23, 2010 17:36
Ola
Quanto a questão do sen^2, separe ele faça sen.sen e derive assim, e alem disso voce pode substitui pq 1/sen é cossec, tente fazer ai qualquer coisa eu ajudo
Ate
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Deivid » Qui Set 23, 2010 18:00
por Deivid » Qui Set 23, 2010 18:00
Olá Maligno, obrigado pela resposta.
Só que, eu não quero derivar, eu quero integrar. Ainda assim tentei e cai em
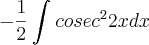
e segundo a tabela que eu tenho a resolução para essa integral se da da seguinte forma:
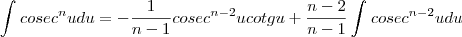
, porém, se eu aplicar a formula, terão varios valores iguais a 0. Como procedo depois de fazer o que você falou?
A a outra duvida sobre a área igual a 0?
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Marcampucio » Qui Set 23, 2010 18:47
por Marcampucio » Qui Set 23, 2010 18:47

quanto à questão da área compreendida entre as curvas, a área abaixo do eixo horizontal produz uma integral negativa. Repare que as áreas são iguais. Você pode optar por:
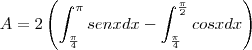
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Deivid » Qui Set 23, 2010 19:35
por Deivid » Qui Set 23, 2010 19:35
Marcumpucio, obrigado pela resposta!
Foi erro meu não ter visto isso na tabela de integrais, eu cismei que era aquela ali que falei no post acima e nem olhei novamente a tabela. Obrigado!
Sobre a área, agora obtive o valor 4.
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Neperiano » Qui Set 23, 2010 19:44
por Neperiano » Qui Set 23, 2010 19:44
Ola
Ops queria falar integral xd, mas o marcopuio ja ajudo
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Deivid » Sáb Set 25, 2010 12:47
por Deivid » Sáb Set 25, 2010 12:47
Eu estava olhando resultados de outras pessoas e elas obtiveram resultados diferentes do meu na questão sobre a área.
Vou postar aqui a minha conta e a conta da outra pessoa que eu olhei.
Resposta da pessoa:


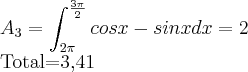
Agora a minha como passaram por aqui:

Qual é a certa?
Obrigado!
-
Deivid
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Set 21, 2010 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Marcampucio » Sáb Set 25, 2010 21:07
por Marcampucio » Sáb Set 25, 2010 21:07
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- deriva simples mais tenho duvida
por vanu » Ter Jan 07, 2014 19:50
- 1 Respostas
- 1098 Exibições
- Última mensagem por anderson_wallace

Ter Jan 07, 2014 22:32
Cálculo: Limites, Derivadas e Integrais
-
- [Quadrado] Duvida quanto a um desafio
por Gilder » Sex Jan 30, 2009 18:12
- 3 Respostas
- 3323 Exibições
- Última mensagem por Sandra Piedade

Ter Fev 03, 2009 08:32
Geometria Plana
-
- Dúvida em polinômio com quadrado perfeito
por Nerd » Seg Set 03, 2012 22:07
- 1 Respostas
- 2055 Exibições
- Última mensagem por Russman

Seg Set 03, 2012 23:05
Polinômios
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3752 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
-
- [Integral] Dúvida com uma integral simples
por Leonardo Ribeiro » Sex Abr 03, 2015 20:02
- 1 Respostas
- 2073 Exibições
- Última mensagem por Leonardo Ribeiro

Sex Abr 03, 2015 21:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para calcular a integral
para calcular a integral 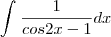 "
" e
e  ,
,  e
e  .Apresente o gráfico da região desenvolvido em um software gráfico."
.Apresente o gráfico da região desenvolvido em um software gráfico."




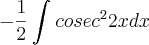 e segundo a tabela que eu tenho a resolução para essa integral se da da seguinte forma:
e segundo a tabela que eu tenho a resolução para essa integral se da da seguinte forma: 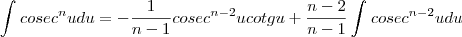 , porém, se eu aplicar a formula, terão varios valores iguais a 0. Como procedo depois de fazer o que você falou?
, porém, se eu aplicar a formula, terão varios valores iguais a 0. Como procedo depois de fazer o que você falou?