 por EulaCarrara » Seg Abr 19, 2010 21:29
por EulaCarrara » Seg Abr 19, 2010 21:29
Alguém poderia me auxiliar nesse exercicio, por favor?

(onde tem-se o simbolo de "+", lê-se: ''pela direita'')
Obrigada

Abraços!
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por EulaCarrara » Seg Abr 19, 2010 21:53
por EulaCarrara » Seg Abr 19, 2010 21:53
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por MarceloFantini » Seg Abr 19, 2010 22:01
por MarceloFantini » Seg Abr 19, 2010 22:01
Vamos analisar
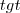
. Quando t se aproxima de

pela direita, os valores vão decrescendo vertiginosamente, tornando a tangente um número extremamente pequeno e
negativo. Isso é importante, pois

, fazendo com que o limite seja

, onde

é elevado a um número muito grande, e dessa maneira o denominador cresce de maneira descontrolada, obrigando a fração a se tornar um valor cada vez mais próximo de zero. Assim:
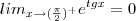
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por EulaCarrara » Seg Abr 19, 2010 22:07
por EulaCarrara » Seg Abr 19, 2010 22:07
Não entendi a parte do a^b = e...
1/(a^b) = 1/e -- (1 sobre A elevado a B = 1 sobre E)
É regra?
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por EulaCarrara » Seg Abr 19, 2010 22:13
por EulaCarrara » Seg Abr 19, 2010 22:13
Ah sim.. agora entendi.
como E está elevado a tg t e tgt é um numero grande e pequeno, entao E estará elevado a este..
Muito obrigada Fantini

-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por MarceloFantini » Seg Abr 19, 2010 23:11
por MarceloFantini » Seg Abr 19, 2010 23:11
Que bom, mas eu quis dizer que a propriedade é que

, que no caso do exercício, era

.
Fico feliz de ter ajudado
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Número de Euler
por Aliocha Karamazov » Sex Out 28, 2011 20:16
- 2 Respostas
- 4332 Exibições
- Última mensagem por Aliocha Karamazov

Sex Out 28, 2011 22:46
Cálculo: Limites, Derivadas e Integrais
-
- UFI- Algarismo da unidade
por Maria Livia » Ter Mar 12, 2013 21:52
- 1 Respostas
- 1589 Exibições
- Última mensagem por DanielFerreira

Ter Mar 12, 2013 22:56
Álgebra Elementar
-
- Encontrar o algarismo das unidades
por jones_slash » Dom Jun 06, 2010 10:42
- 2 Respostas
- 3610 Exibições
- Última mensagem por jones_slash

Seg Jun 07, 2010 22:44
Álgebra Elementar
-
- [Aritmética] Algarismo das unidades
por Russman » Qui Jan 17, 2013 01:28
- 4 Respostas
- 7321 Exibições
- Última mensagem por DanielFerreira

Qui Jan 17, 2013 06:58
Aritmética
-
- Algarismo que ocupa a ordem das unidades
por Cleyson007 » Dom Jan 10, 2010 18:28
- 1 Respostas
- 9434 Exibições
- Última mensagem por MarceloFantini

Dom Jan 10, 2010 20:43
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







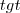 . Quando t se aproxima de
. Quando t se aproxima de  pela direita, os valores vão decrescendo vertiginosamente, tornando a tangente um número extremamente pequeno e negativo. Isso é importante, pois
pela direita, os valores vão decrescendo vertiginosamente, tornando a tangente um número extremamente pequeno e negativo. Isso é importante, pois  , fazendo com que o limite seja
, fazendo com que o limite seja  , onde
, onde  é elevado a um número muito grande, e dessa maneira o denominador cresce de maneira descontrolada, obrigando a fração a se tornar um valor cada vez mais próximo de zero. Assim:
é elevado a um número muito grande, e dessa maneira o denominador cresce de maneira descontrolada, obrigando a fração a se tornar um valor cada vez mais próximo de zero. Assim: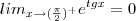





 , que no caso do exercício, era
, que no caso do exercício, era  .
.


 .
.



