 por matmatco » Sex Abr 12, 2013 23:00
por matmatco » Sex Abr 12, 2013 23:00
Tentei substituir na soma esses dados mas é errado eu fazer isso, não estou sabendo como resolver
Sejam f(t),g(t) h(t) funções deriváveis em R e tais que para todo t,
f '(t)=g(t)
g'(t)= -f(t) - h(t)
h'(t)=g(t)
suponha que f(0)=g(0)=h(0)=1. prove que para todo t, [f(t)]²+[g(t)]²+h[(t)]²=3
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por young_jedi » Sáb Abr 13, 2013 15:17
por young_jedi » Sáb Abr 13, 2013 15:17
derivando a segunda equação nos temos

substittuindo as outras duas equações nos temos

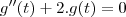
este é uma equação diferencial de segunda ordem resolvendo ela se encontra g(t) e depois h(t) e f(t)
comente qualquer coisa
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por matmatco » Sáb Abr 13, 2013 16:06
por matmatco » Sáb Abr 13, 2013 16:06
ok, mas para encontrar o g(t) vou ter que jogar valores para g(t)? é isso? e depois derivar para encontrar o g"(t)?
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por young_jedi » Sáb Abr 13, 2013 16:32
por young_jedi » Sáb Abr 13, 2013 16:32
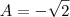
esta equação diferencial de segunda ordem tem como resposta algo do tipo
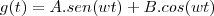
ao substituindo isto na equação diferencial, voce vai determinar o valor de w, e depois com g(0)=1 voce determina os valores de A e B e as funções h(t) e f(t)
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por matmatco » Sáb Abr 13, 2013 22:51
por matmatco » Sáb Abr 13, 2013 22:51
estou com dificuldade em colocar os calculos então vou deixar os valores que encontrei depois com mais calma e se eu conseguir coloco a resolução.
resolvendo encontrei w=
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
, usando g(0) achei A= 0 e B=1.Com isso encontro g(t)=1.
Depois usando a equação g`(t)= -f(t)-h(t) e usando g'(t)=Asen(wt)w-Bcos(wt)w que é a derivada da equação que você disse, acho
g'(t)=0.
com isso substituindo na equação g'(t)= -f(t)-h(t)
f(t)=1 e assim encontro que h(t) = 1 portanto f(t)²+g(t)²+h(t)²= 1²+1²+1²= 3.
meus calculos estão certos?
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por young_jedi » Dom Abr 14, 2013 11:23
por young_jedi » Dom Abr 14, 2013 11:23
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por matmatco » Dom Abr 14, 2013 13:19
por matmatco » Dom Abr 14, 2013 13:19
entendi, mas não sabia que ia ter que integrar o f ' (t) para achar o valor de A e sobre as constantes eu já não poderia elimina-las sem ter que encontrar seus valores?
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por young_jedi » Dom Abr 14, 2013 15:24
por young_jedi » Dom Abr 14, 2013 15:24
voce não pode eliminar as constantes direto, neste caso elas eram iguais a zero, mais em outros casos pode ser que não
então voce tem que encontra-las, e a constante A é a mesma coisa voce tem que integrar f'(t) e h'(t) e utilizar a relação
g(0)=g(0)=h(0)=1 para determina-la.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por matmatco » Dom Abr 14, 2013 19:52
por matmatco » Dom Abr 14, 2013 19:52
ok, muito obrigado
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relação entre funções, sequências e regressões
 por Jhenrique » Qui Set 20, 2012 00:14
por Jhenrique » Qui Set 20, 2012 00:14
- 52 Respostas
- 40265 Exibições
- Última mensagem por MarceloFantini

Qua Out 31, 2012 19:50
Funções
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 2054 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:00
Trigonometria
-
- relação entre x e y
por Apotema » Qua Nov 18, 2009 19:57
- 4 Respostas
- 5857 Exibições
- Última mensagem por Apotema

Seg Nov 23, 2009 08:12
Trigonometria
-
- relação entre a e b
por jose henrique » Seg Set 13, 2010 09:31
- 3 Respostas
- 4707 Exibições
- Última mensagem por Elcioschin

Ter Set 14, 2010 10:45
Álgebra Elementar
-
- [relação entre PA e PG]
por JKS » Qui Abr 11, 2013 01:11
- 2 Respostas
- 3474 Exibições
- Última mensagem por JKS

Dom Abr 21, 2013 18:07
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




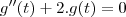

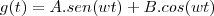
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) , usando g(0) achei A= 0 e B=1.Com isso encontro g(t)=1.
, usando g(0) achei A= 0 e B=1.Com isso encontro g(t)=1. estea certo
estea certo 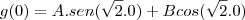







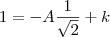

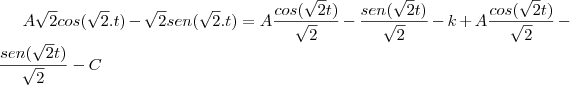
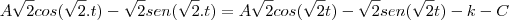
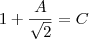

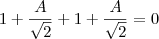



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.