Tentei substituir na soma esses dados mas é errado eu fazer isso, não estou sabendo como resolver
Sejam f(t),g(t) h(t) funções deriváveis em R e tais que para todo t,
f '(t)=g(t)
g'(t)= -f(t) - h(t)
h'(t)=g(t)
suponha que f(0)=g(0)=h(0)=1. prove que para todo t, [f(t)]²+[g(t)]²+h[(t)]²=3




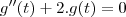

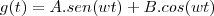
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) , usando g(0) achei A= 0 e B=1.Com isso encontro g(t)=1.
, usando g(0) achei A= 0 e B=1.Com isso encontro g(t)=1. estea certo
estea certo 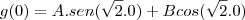







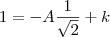

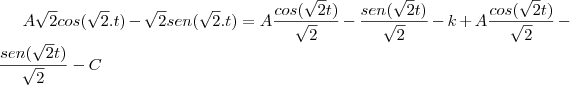
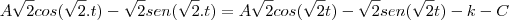
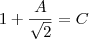

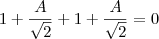
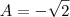



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)