Por exemplo: fazendo o desenvolvimento desse limite
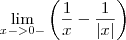 (I)
(I)** obs: x tende a zero pela esquerda
cheguei em
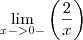 (II)
(II)daí, imaginei que a resposta seria MENOS INFINITO.
Porém, no livro, diz que esse limite não existe.
Fui checar no site "wolframalpha" e a resposta dá MENOS INFINITO.
Enfim, qual a diferença em um limite não existir e um limite que resulta em mais ou menos infinito?? São coisas sinônimas??? Caso sejam coisas diferentes, como saber quando vai ocorrer um ou outro ??
Estou ligada que um limite não existe quando os limites laterais são diferentes, por exemplo,o limite de (II) citado acima ,quando x tende a zero (desconsiderando
então o sinal que indica o limite lateral) , não existe pois os limites laterais são diferentes (um tende a menos infinito e o outro a mais infinito de acordo com o
site "wolframalpha")... Ah, para quem for me responder, calcule o outro limite lateral da equação (I) para ajudar no meu entendimento, por gentileza ^^
Aguardando a explicação ^^ bj!!




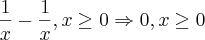
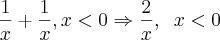



 .
.



