
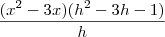
o que falta? estou certo?? a partir do primeiro igual fui eu que fiz...
obrigado!


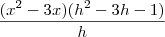

 não é uma variável, é apenas um artifício algébrico para cálcular a função derivada da
não é uma variável, é apenas um artifício algébrico para cálcular a função derivada da  .
.![[f(x)+g(x)]'=f'(x)+g'(x) [f(x)+g(x)]'=f'(x)+g'(x)](/latexrender/pictures/42d4692b5412eda2775446cd6ee1cf4b.png)
![[k\cdot f(x)]'=k\cdot[f(x)]' [k\cdot f(x)]'=k\cdot[f(x)]'](/latexrender/pictures/a35e7df96d78ada8a1eae6152fbf1e37.png)
![f'(x)=[x^2]'+[-3x]'=2x-3 f'(x)=[x^2]'+[-3x]'=2x-3](/latexrender/pictures/9161a9a0e54fc21f7d85efdf9fcc45fb.png)




MarceloFantini escreveu:
Isto não é verdade. Note que, assim
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)