 por mih123 » Ter Set 18, 2012 12:56
por mih123 » Ter Set 18, 2012 12:56
Olá, não sei resolver esse limite.Não sei nem a resposta.. ;/
![\lim_{x\to\infty}\left[\frac{1}{\sqrt[2]{{n}^{2}+1}}+ \frac{1}{\sqrt[2]{{n}^{2}+2}}+\frac{1}{\sqrt[2]{{n}^{2}+3}}+...+\frac{1}{\sqrt[2]{{n}^{2}+n}}\right]} \lim_{x\to\infty}\left[\frac{1}{\sqrt[2]{{n}^{2}+1}}+ \frac{1}{\sqrt[2]{{n}^{2}+2}}+\frac{1}{\sqrt[2]{{n}^{2}+3}}+...+\frac{1}{\sqrt[2]{{n}^{2}+n}}\right]}](/latexrender/pictures/59555e4a6d61612684fbc6fe55bb5681.png)
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Ter Set 18, 2012 13:39
por young_jedi » Ter Set 18, 2012 13:39
Só uma duvida, é limite de x tendendo ao infinito ou seria limite de n tendendo ao infinito?
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por mih123 » Ter Set 18, 2012 14:00
por mih123 » Ter Set 18, 2012 14:00
Então, na questão está x tendendo a infinito,mas eu acho que seria n tendendo a infinito.
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Renato_RJ » Ter Set 18, 2012 14:13
por Renato_RJ » Ter Set 18, 2012 14:13
Estou um tanto confuso com essa questão... O termo

não parece ser o mesmo n do último termo, veja como eu estou entendendo essa série:

E isso é muito estranho (ao menos para mim)....
Tem como rever a questão detalhadamente ?? Tipo, algo no enunciado por exemplo....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por young_jedi » Ter Set 18, 2012 14:15
por young_jedi » Ter Set 18, 2012 14:15
temos que

mas

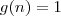
temos tambem que

mas
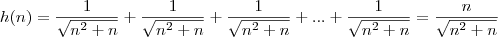
mas

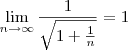
pelo teorema do confronto se

e
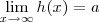
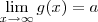
então
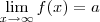
com isso temos

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por mih123 » Ter Set 18, 2012 14:36
por mih123 » Ter Set 18, 2012 14:36
No enunciado diz apenas pra determinar o limite.Quando tiver aula novamente com o professor eu pergunto.
Valew

-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Renato_RJ » Ter Set 18, 2012 14:53
por Renato_RJ » Ter Set 18, 2012 14:53
mih123 escreveu:No enunciado diz apenas pra determinar o limite.Quando tiver aula novamente com o professor eu pergunto.
Valew

Opa, o colega Young_Jedi matou a questão !!
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por mih123 » Ter Set 18, 2012 15:11
por mih123 » Ter Set 18, 2012 15:11
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Ter Set 18, 2012 15:15
por young_jedi » Ter Set 18, 2012 15:15
porque ai voce so colocou quatro termos da serie
mais a quantidades de termos depende de n tambem
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por mih123 » Qua Set 19, 2012 02:17
por mih123 » Qua Set 19, 2012 02:17
young_jedi escreveu:temos que

mas

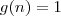
temos tambem que

mas
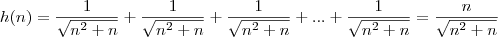
mas

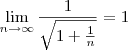
pelo teorema do confronto se

e
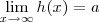
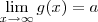
então
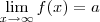
com isso temos

Boa Noite, Young_jedi estou muito confusa com sua resolução, não consegui entender porque ficou
![\frac{1}{\sqrt[2]{{n}^{2}}} \frac{1}{\sqrt[2]{{n}^{2}}}](/latexrender/pictures/992bc21124b78030dd046d5bf3d7a435.png)
e na outra função
![\frac{1} {\sqrt[2]{{n}^{2}+n}} \frac{1} {\sqrt[2]{{n}^{2}+n}}](/latexrender/pictures/9e6a1c079abe75698c34de12a0f142e5.png)
??
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qua Set 19, 2012 02:27
por MarceloFantini » Qua Set 19, 2012 02:27
Ele não falou que é igual, e sim que é menor. Note que
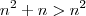
para todo valor natural, então

e

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por mih123 » Qua Set 19, 2012 13:55
por mih123 » Qua Set 19, 2012 13:55
Ahh sim. Olhei direitinho, entendi! Muito Obrigada.
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4796 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5127 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7270 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to\infty}\left[\frac{1}{\sqrt[2]{{n}^{2}+1}}+ \frac{1}{\sqrt[2]{{n}^{2}+2}}+\frac{1}{\sqrt[2]{{n}^{2}+3}}+...+\frac{1}{\sqrt[2]{{n}^{2}+n}}\right]} \lim_{x\to\infty}\left[\frac{1}{\sqrt[2]{{n}^{2}+1}}+ \frac{1}{\sqrt[2]{{n}^{2}+2}}+\frac{1}{\sqrt[2]{{n}^{2}+3}}+...+\frac{1}{\sqrt[2]{{n}^{2}+n}}\right]}](/latexrender/pictures/59555e4a6d61612684fbc6fe55bb5681.png)


![\lim_{x\to\infty}\left[\frac{1}{\sqrt[2]{{n}^{2}+1}}+ \frac{1}{\sqrt[2]{{n}^{2}+2}}+\frac{1}{\sqrt[2]{{n}^{2}+3}}+...+\frac{1}{\sqrt[2]{{n}^{2}+n}}\right]} \lim_{x\to\infty}\left[\frac{1}{\sqrt[2]{{n}^{2}+1}}+ \frac{1}{\sqrt[2]{{n}^{2}+2}}+\frac{1}{\sqrt[2]{{n}^{2}+3}}+...+\frac{1}{\sqrt[2]{{n}^{2}+n}}\right]}](/latexrender/pictures/59555e4a6d61612684fbc6fe55bb5681.png)



 não parece ser o mesmo n do último termo, veja como eu estou entendendo essa série:
não parece ser o mesmo n do último termo, veja como eu estou entendendo essa série:



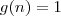

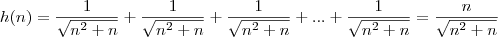

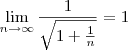

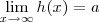
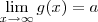
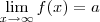







![\frac{1}{\sqrt[2]{{n}^{2}}} \frac{1}{\sqrt[2]{{n}^{2}}}](/latexrender/pictures/992bc21124b78030dd046d5bf3d7a435.png) e na outra função
e na outra função ![\frac{1} {\sqrt[2]{{n}^{2}+n}} \frac{1} {\sqrt[2]{{n}^{2}+n}}](/latexrender/pictures/9e6a1c079abe75698c34de12a0f142e5.png) ??
??
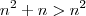 para todo valor natural, então
para todo valor natural, então  e
e  .
.

