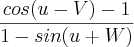
calcular as primeiras derivadas e o seu gradiente,encontrar um ponto onde f se anule ou não.
vou considerar cos(u-v) como um todo e é cos (x) ou vou ter que dizer que cos(u-v)= cosu.cosv+sinu.sinv e tambem não sei o que faço com o -1.
E no denominador tenho de fazer o mesmo? colocar as equivalências trignométricas ou não? faço a derivação do quociente directamente, mas novamente tenho de achar as 3 derivadas de cada vez,não consigo encontrar nada que me explique isso em condições estou feito.
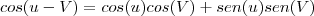, você vai precisar também de 
.
.
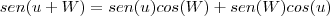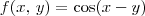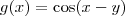(isto é, depende apenas de x).![\frac{\partial f}{\partial x} = \frac{d g}{d x} = \left[-\textrm{sen}\,(x-y) \right] \cdot \frac{d}{d x}(x-y) = \left[-\textrm{sen}\,(x-y) \right] \cdot 1 = -\textrm{sen}\,(x-y)](/latexrender/pictures/d4e032097c25fbdb93f3e7e09020f00c.png "\frac{\partial f}{\partial x} = \frac{d g}{d x} = \left[-\textrm{sen}\,(x-y) \right] \cdot \frac{d}{d x}(x-y) = \left[-\textrm{sen}\,(x-y) \right] \cdot 1 = -\textrm{sen}\,(x-y)")
(isto é, depende apenas de y).![\frac{\partial f}{\partial y} = \frac{d g}{d y} = \left[-\textrm{sen}\,(x-y) \right] \cdot \frac{d}{d y}(x-y) = \left[-\textrm{sen}\,(x-y) \right] \cdot (-1) = \textrm{sen}\,(x-y)](/latexrender/pictures/604e3d42e14dbcd7e48ffd2b9a62078b.png "\frac{\partial f}{\partial y} = \frac{d g}{d y} = \left[-\textrm{sen}\,(x-y) \right] \cdot \frac{d}{d y}(x-y) = \left[-\textrm{sen}\,(x-y) \right] \cdot (-1) = \textrm{sen}\,(x-y)")
por 