 por caiofisico » Qui Out 27, 2011 13:12
por caiofisico » Qui Out 27, 2011 13:12
to com uma duvida na questao abaixo, preciso de uma ajuda
4- determine os pontos da curva 5x^2 - 6xy + 5y^2 = 4 mais proximos da origem.
Obrigado
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Neperiano » Qui Out 27, 2011 14:14
por Neperiano » Qui Out 27, 2011 14:14
Ola
Não sei se da pra resolver por limite, mas seria interessante tentar, x e y tendendo a 0
Ou pode ir chutando valores até descobrir o mais perto
Deve ter outro jeito mas eu só sei fazer por estes dois
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por caiofisico » Qui Out 27, 2011 15:05
por caiofisico » Qui Out 27, 2011 15:05
Eu poderia por exemplo derivar e igualar a zero?
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Neperiano » Qui Out 27, 2011 15:13
por Neperiano » Qui Out 27, 2011 15:13
Ola
Até pode mas não sei se vai ajudar muito, ficaria:
10x-6y+6x+10y=0
Se quise tentar
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por caiofisico » Qui Out 27, 2011 15:38
por caiofisico » Qui Out 27, 2011 15:38
Vou tentar, mais eu poderia fazer pitagoras e aplicar na formula d^2 = x^2 + y^2 e depois derivar d
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Qui Out 27, 2011 17:00
por LuizAquino » Qui Out 27, 2011 17:00
Olá caiofisico,
Esse exercício foi proposto em que parte do conteúdo da disciplina?
Você já estudou como calcular o máximo (ou o mínimo) de funções com duas variáveis? Ou de funções com apenas uma?
Ou por acaso esse exercício foi proposto na disciplina de Geometria Analítica? Nesse contexto, você já estou sobre mudança de coordenadas (rotação e translação de eixos)?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por caiofisico » Qui Out 27, 2011 20:04
por caiofisico » Qui Out 27, 2011 20:04
já tivemos máximos e mínimos sim, eu fiz assim

![y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10} y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10}](/latexrender/pictures/0e7640e489e40d9589209bcf5fa4520b.png)
![y=\frac{3x +/- 2\sqrt[]{5-4x}}{5} y=\frac{3x +/- 2\sqrt[]{5-4x}}{5}](/latexrender/pictures/6706708f9b4e083b72f4403128e95b1b.png)
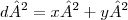
dai depois derivo d, to com dificuldade nessa parte da derivação, também não sei se essa forma que eu fiz esta correta =/
** saiu errado no editor o ² é elevado ao quadrado ^^
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Qui Out 27, 2011 22:27
por LuizAquino » Qui Out 27, 2011 22:27
caiofisico escreveu:já tivemos máximos e mínimos sim
Ok. Mas no caso, para funções com 1 ou 2 variáveis? Esse exercício sairia mais fácil por funções de duas variáveis, mas se você está em Cálculo I provavelmente viu apenas o máximo ou mínimo de funções com 1 variável.
Para usar uma função de apenas 1 variável, é por aí mesmo. Entretanto, note que:
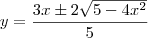
Agora você vai montar duas funções:

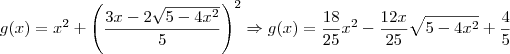
Será necessário determinar o mínimo de cada uma delas.
caiofisico escreveu:dai depois derivo d, to com dificuldade nessa parte da derivação (...)
Como exemplo, veja a derivada de
f:
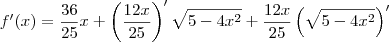
![f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right] f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right]](/latexrender/pictures/63a7ae7e395d1909ebc3d9e8aff25543.png)

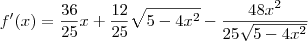 Observação
ObservaçãoO carácter  que apareceu na sua mensagem deve-se ao fato de você ter usado o atalho do teclado para digitar o quadrado no LaTeX, isto é, você escreveu algo como x². O correto seria usar o comando x^2 dentro do LaTeX. Isso produz como resultado:

.
Além disso, aproveito para dizer que o símbolo de "mais ou menos" no LaTeX é obtido pelo comando \pm:
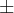
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por caiofisico » Sex Out 28, 2011 20:10
por caiofisico » Sex Out 28, 2011 20:10
obrigado amigo, consegui chegar ao resultado pela forma que vc me explicou, os pontos são (x=0,5 y=-0,5) ; (x=-0,5; y= 0,5)
-
caiofisico
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Ago 20, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Achar os pontos sobre a curva
por Fernandobertolaccini » Sex Jul 04, 2014 13:37
- 1 Respostas
- 1393 Exibições
- Última mensagem por young_jedi

Sáb Jul 05, 2014 15:26
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo]classe da curva, significado
por Camolas » Sex Mai 31, 2013 14:51
- 0 Respostas
- 1221 Exibições
- Última mensagem por Camolas

Sex Mai 31, 2013 14:51
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de vetor normal à curva de equação.
por Sobreira » Qua Mar 20, 2013 09:36
- 3 Respostas
- 3428 Exibições
- Última mensagem por Sobreira

Sex Mar 22, 2013 14:38
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2] Função vetorial e curva espacial
por NavegantePI » Qua Mai 18, 2016 01:08
- 0 Respostas
- 2160 Exibições
- Última mensagem por NavegantePI

Qua Mai 18, 2016 01:08
Geometria Espacial
-
- Calculo Distancia Entre dois pontos
por AndyPere » Seg Abr 05, 2010 12:22
- 0 Respostas
- 3184 Exibições
- Última mensagem por AndyPere

Seg Abr 05, 2010 12:22
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









![y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10} y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10}](/latexrender/pictures/0e7640e489e40d9589209bcf5fa4520b.png)
![y=\frac{3x +/- 2\sqrt[]{5-4x}}{5} y=\frac{3x +/- 2\sqrt[]{5-4x}}{5}](/latexrender/pictures/6706708f9b4e083b72f4403128e95b1b.png)
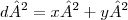

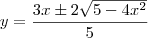

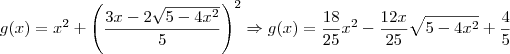
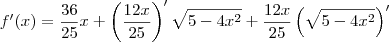
![f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right] f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right]](/latexrender/pictures/63a7ae7e395d1909ebc3d9e8aff25543.png)

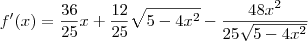
 .
.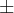 .
.
