to com uma duvida na questao abaixo, preciso de uma ajuda
4- determine os pontos da curva 5x^2 - 6xy + 5y^2 = 4 mais proximos da origem.
Obrigado









![y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10} y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10}](/latexrender/pictures/0e7640e489e40d9589209bcf5fa4520b.png)
![y=\frac{3x +/- 2\sqrt[]{5-4x}}{5} y=\frac{3x +/- 2\sqrt[]{5-4x}}{5}](/latexrender/pictures/6706708f9b4e083b72f4403128e95b1b.png)
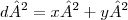

caiofisico escreveu:já tivemos máximos e mínimos sim
eu fiz assim
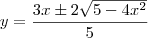

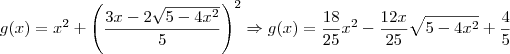
caiofisico escreveu:dai depois derivo d, to com dificuldade nessa parte da derivação (...)
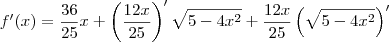
![f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right] f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right]](/latexrender/pictures/63a7ae7e395d1909ebc3d9e8aff25543.png)

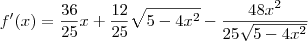
 .
. .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)