caiofisico escreveu:já tivemos máximos e mínimos sim
Ok. Mas no caso, para funções com 1 ou 2 variáveis? Esse exercício sairia mais fácil por funções de duas variáveis, mas se você está em Cálculo I provavelmente viu apenas o máximo ou mínimo de funções com 1 variável.
Para usar uma função de apenas 1 variável, é por aí mesmo. Entretanto, note que:
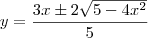
Agora você vai montar duas funções:

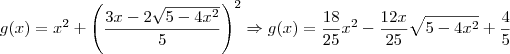
Será necessário determinar o mínimo de cada uma delas.
caiofisico escreveu:dai depois derivo d, to com dificuldade nessa parte da derivação (...)
Como exemplo, veja a derivada de
f:
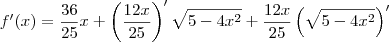
![f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right] f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right]](/latexrender/pictures/63a7ae7e395d1909ebc3d9e8aff25543.png)

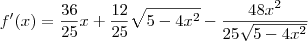 Observação
ObservaçãoO carácter  que apareceu na sua mensagem deve-se ao fato de você ter usado o atalho do teclado para digitar o quadrado no LaTeX, isto é, você escreveu algo como x². O correto seria usar o comando x^2 dentro do LaTeX. Isso produz como resultado:

.
Além disso, aproveito para dizer que o símbolo de "mais ou menos" no LaTeX é obtido pelo comando \pm:
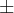
.









![y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10} y=\frac{6x +/- \sqrt[]{36x²-20(5x²-4)}}{10}](/latexrender/pictures/0e7640e489e40d9589209bcf5fa4520b.png)
![y=\frac{3x +/- 2\sqrt[]{5-4x}}{5} y=\frac{3x +/- 2\sqrt[]{5-4x}}{5}](/latexrender/pictures/6706708f9b4e083b72f4403128e95b1b.png)
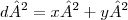

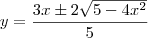

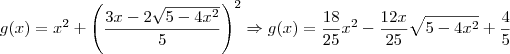
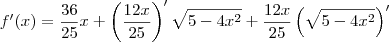
![f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right] f^\prime(x) = \frac{36}{25}x + \frac{12}{25}\sqrt{5-4x^2} + \frac{12x}{25}\left[\frac{1}{2\sqrt{5-4x^2}}\left(5-4x^2\right)^\prime\right]](/latexrender/pictures/63a7ae7e395d1909ebc3d9e8aff25543.png)

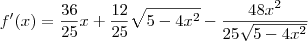
 .
. .
.


 .
.



