![f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a] f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a]](/latexrender/pictures/dee6474fa65c3b4a6c39e54d8c8531a7.png)


![f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a] f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a]](/latexrender/pictures/dee6474fa65c3b4a6c39e54d8c8531a7.png)

maykonnunes escreveu:Encontre a área da superfície formada pela rotação, ao redor do eixo x, do gráfico da função,
![S = \int_{0}^{a} 2\pi f(x) \sqrt{1 + [f^\prime(x)]^2}\,dx S = \int_{0}^{a} 2\pi f(x) \sqrt{1 + [f^\prime(x)]^2}\,dx](/latexrender/pictures/fd3416f8ca23636de00b3734a78844c3.png)
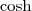 ) é definido como:
) é definido como: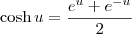
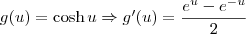
![\sqrt{1 + [g^\prime(u)]^2} = \sqrt{1 + \left(\frac{e^u - e^{-u}}{2}\right)^2} \sqrt{1 + [g^\prime(u)]^2} = \sqrt{1 + \left(\frac{e^u - e^{-u}}{2}\right)^2}](/latexrender/pictures/feede8311f2f939785db2f327f3070e9.png)

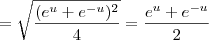
 ) é definido como:
) é definido como: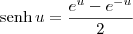
![[\cosh u]^\prime = \textrm{senh}\, u [\cosh u]^\prime = \textrm{senh}\, u](/latexrender/pictures/f22768b9f29e98207b507f554673cf07.png)
![[\textrm{senh}\, u]^\prime = \cosh u [\textrm{senh}\, u]^\prime = \cosh u](/latexrender/pictures/53536557cb2a98b2f13ab397339f2452.png)


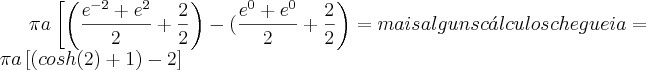

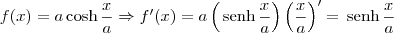

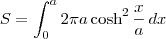
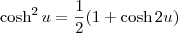 .
.
 e
e  .
.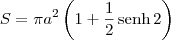

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.