 por Anne2011 » Sex Set 16, 2011 16:26
por Anne2011 » Sex Set 16, 2011 16:26
Tô com problemas para chegar no resultado dessa integral:
![\frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}} \frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}}](/latexrender/pictures/d5cc0c10e0da7530d669bbf7db7d9a2f.png)
, t>1, v(2)=0
Integrando cheguei a esse resultado:
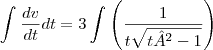
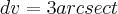
No livro, a resposta é

...
De onde raios saiu esse


e não consegui tirar essa  de dentro da raiz tbm não rsrsrs... Alguem poderia me ajudar???
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 17:22
por MarceloFantini » Sex Set 16, 2011 17:22
Talvez seja da condição inicial, pois na resolução da integral o resultado será

, mas com a condição você encontra o valor de K.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Anne2011 » Sex Set 16, 2011 17:48
por Anne2011 » Sex Set 16, 2011 17:48
A condição inicial é t>1, v(2)=0, substituindo o valor de t do resultado por 2 (e eu sou pessima em arcs), significa então que o resultado de K seria esse:
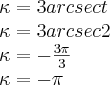
Uma conclusão lógica apenas, não faço a mais minima ideia de pq
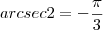
...
Alguem aí com uma luz para mim???
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 18:02
por MarceloFantini » Sex Set 16, 2011 18:02
A função

lê-se "o arco cuja secante é t", ou seja, você tem um ângulo

tal que
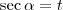
. Vamos ao exercício para facilitar o entendimento: se

então

, mas
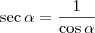
e daí

. O valor de

que satisfaz é

, e portanto
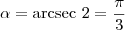
. Então, temos
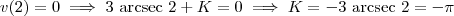
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Anne2011 » Sex Set 16, 2011 18:53
por Anne2011 » Sex Set 16, 2011 18:53
Obrigado Fantini vou copiar isso, tô apanhando aqui com as integrais que envolvem os arcos... tenho que dedicar um tempo extra às relações trigonométricas.
-
Anne2011
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qui Jun 23, 2011 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecanica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Problemas de Valor Inicial] Equações Diferenciais
por mayconf » Ter Abr 15, 2014 18:24
- 1 Respostas
- 2113 Exibições
- Última mensagem por Russman

Ter Abr 15, 2014 22:28
Equações
-
- [Equação diferencial] Problema de valor inicial
por Aliocha Karamazov » Qua Fev 15, 2012 23:34
- 2 Respostas
- 1793 Exibições
- Última mensagem por Aliocha Karamazov

Qui Fev 23, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais - problema de valor inicial
por emsbp » Qui Abr 12, 2012 18:14
- 0 Respostas
- 1023 Exibições
- Última mensagem por emsbp

Qui Abr 12, 2012 18:14
Cálculo: Limites, Derivadas e Integrais
-
- (calculo III) resolva o seguinte problema de valor inicial
 por liviabgomes » Qui Dez 01, 2011 14:59
por liviabgomes » Qui Dez 01, 2011 14:59
- 4 Respostas
- 2358 Exibições
- Última mensagem por liviabgomes

Seg Dez 05, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Determinar a velocidade inicial
por alexandre32100 » Ter Mar 15, 2011 00:31
- 1 Respostas
- 2756 Exibições
- Última mensagem por Elcioschin

Ter Mar 15, 2011 14:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}} \frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}}](/latexrender/pictures/d5cc0c10e0da7530d669bbf7db7d9a2f.png) , t>1, v(2)=0
, t>1, v(2)=0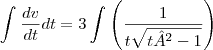
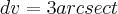
 ...
...

![\frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}} \frac{dv}{dt}=\frac{3}{t \sqrt[]{t²-1}}](/latexrender/pictures/d5cc0c10e0da7530d669bbf7db7d9a2f.png) , t>1, v(2)=0
, t>1, v(2)=0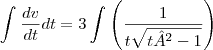
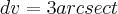
 ...
...

 , mas com a condição você encontra o valor de K.
, mas com a condição você encontra o valor de K.

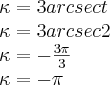
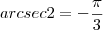 ...
...
 lê-se "o arco cuja secante é t", ou seja, você tem um ângulo
lê-se "o arco cuja secante é t", ou seja, você tem um ângulo  tal que
tal que 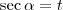 . Vamos ao exercício para facilitar o entendimento: se
. Vamos ao exercício para facilitar o entendimento: se  então
então  , mas
, mas 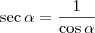 e daí
e daí  . O valor de
. O valor de  que satisfaz é
que satisfaz é  , e portanto
, e portanto 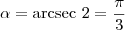 . Então, temos
. Então, temos 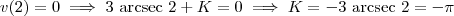 .
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.