Primeiro, note que a reta tangente a qualquer ponto da parábola toca essa parábola em apenas um ponto. Isso não acontece em outras curvas. Por exemplo, a reta tangente ao gráfico de f(x) = x³ no ponto (1, 1) também toca o ponto (-2, -8).
Dito isso, observe que a reta tangente a

no ponto (
k,
f(
k)), e que passa pelo ponto (2, 9), é dada por:

Ou seja, temos a equação dessa reta dada por:

Essa reta deve tocar apenas um ponto da parábola
f. Isso significa que o valor de
k é tal que a equação a seguir só tem uma única solução para
x:

Arrumando essa equação, obtemos:

Para que essa equação tenha apenas uma solução para
x, é necessário que o seu discriminante (isto é, seu

) seja 0. Com essa informação você determina os possíveis valores de
k e consequentemente as possíveis retas tangentes.
 e que passa pelo ponto (2,9).
e que passa pelo ponto (2,9).
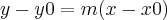
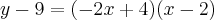
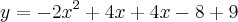



 .Senão vejamos:
.Senão vejamos: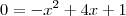




 pertence ao gráfico, mas que o objetivo seja encontrar retas tangentes ao gráfico e que também passem por esse ponto.
pertence ao gráfico, mas que o objetivo seja encontrar retas tangentes ao gráfico e que também passem por esse ponto.


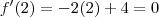
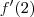 significa a reta tangente a parábola no ponto 2, que não necessariamente é a reta tangente que também passa por
significa a reta tangente a parábola no ponto 2, que não necessariamente é a reta tangente que também passa por  no ponto (
no ponto (



 ) seja 0. Com essa informação você determina os possíveis valores de
) seja 0. Com essa informação você determina os possíveis valores de 

 , avisa que eu resolvo.
, avisa que eu resolvo.

