nao consegui compreendê-la
http://pt.wikipedia.org/wiki/Regra_de_l%27H%C3%B4pital
Por exemplo, como aplicar ela nesse limite
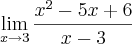
obrigado

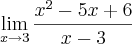





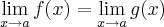 . (Um dos casos)
. (Um dos casos)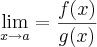 , só poderei aplicar essa regra, se, tanto f(x) quanto f(x) tenderem para o mesmo 'lugar'.
, só poderei aplicar essa regra, se, tanto f(x) quanto f(x) tenderem para o mesmo 'lugar'.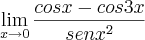
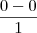 poderei aplicar a regra do L'Hopital?
poderei aplicar a regra do L'Hopital?



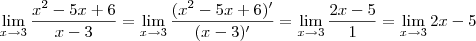
 é uma função contínua, então:
é uma função contínua, então:


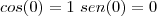
 . Então é possível utilizar L'Hopital. Que resulta em:
. Então é possível utilizar L'Hopital. Que resulta em:
 , então aplique L'Hopital de novo:
, então aplique L'Hopital de novo:





 .
.


 e apliquei a regra do L'Hopital derivando f(x) e g(x) (Em cima e Embaixo, respectivamente).
e apliquei a regra do L'Hopital derivando f(x) e g(x) (Em cima e Embaixo, respectivamente).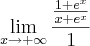


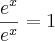 .
.
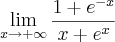

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes