 por fernandocez » Ter Nov 20, 2012 22:28
por fernandocez » Ter Nov 20, 2012 22:28
Olá pessoal, estou tentando resolver essa questão. Prova do Bombeiro 2002.
36. Em um terreno retangular, como mostra a figura abaixo, foi construída uma oficina de formato triangular (triângulo retângulo). O polinômio que expressa a área não construída (escura) deste terreno é:
a) 20 x² + 12x
b) 20 x² + 8x
c) 20 x² + 16x
d) 25x² + 12x
e)
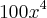
+


Eu calculei a área total
At = (5x + 4)4x = 20x² + 16x
faltou calcular a área do triângulo (polinômio) para subtrair da área total.
Marquei mas alguns valores na figura mas não consegui evoluir disso. A resposta certa é: (a)
Agradeço quem puder ajudar.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por MarceloFantini » Qua Nov 21, 2012 00:43
por MarceloFantini » Qua Nov 21, 2012 00:43
Ele dá o comprimento destas pequenas setas? Porque se sim, a área do triângulo será
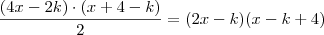
. Com o valor de

, que é este comprimento, você substitui e encontrará o outro polinômio, bastando subtrair da área total.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fernandocez » Qua Nov 21, 2012 16:08
por fernandocez » Qua Nov 21, 2012 16:08
A questão não tem mais nenhuma informação. Eu também achei estranho, parece que tá faltando alguma informação a mais. Mesmo assim obrigado por tentar.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Seg Nov 26, 2012 21:01
por fernandocez » Seg Nov 26, 2012 21:01
Alguem tem ideia pra resolver essa questão? Parece sem solução mas se alguém tiver uma dica ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por MarceloFantini » Seg Nov 26, 2012 21:06
por MarceloFantini » Seg Nov 26, 2012 21:06
Fernando, você pode tirar uma foto com a questão inteira? Quem sabe falta algum pedaço, não sei. Vale a pena tentar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Seg Nov 26, 2012 22:20
por e8group » Seg Nov 26, 2012 22:20
Calculei

.
Resolução :
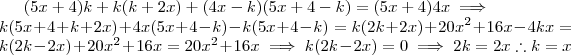
.
Daí ,

.
Tem gabarito ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fernandocez » Qua Nov 28, 2012 17:18
por fernandocez » Qua Nov 28, 2012 17:18
Tem sim Santhiago. Alias, obrigado pela ajuda.
A opção certa é a que vc encontrou.
a) 20x² + 12x
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Qua Nov 28, 2012 18:21
por fernandocez » Qua Nov 28, 2012 18:21
MarceloFantini escreveu:Fernando, você pode tirar uma foto com a questão inteira? Quem sabe falta algum pedaço, não sei. Vale a pena tentar.
Oi Marcelo. A figura da prova tá completa. Obrigado pelo interesse.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] Área
 por Micael » Ter Mai 14, 2013 22:19
por Micael » Ter Mai 14, 2013 22:19
- 1 Respostas
- 2073 Exibições
- Última mensagem por Molina

Qua Mai 15, 2013 00:51
Geometria Espacial
-
- [geometria plana] Area e Volume
 por Erikax » Sáb Jul 19, 2014 15:23
por Erikax » Sáb Jul 19, 2014 15:23
- 0 Respostas
- 2049 Exibições
- Última mensagem por Erikax

Sáb Jul 19, 2014 15:23
Geometria Plana
-
- [GEOMETRIA PLANA] Cálculo de área
 por eulalia » Seg Abr 20, 2015 16:40
por eulalia » Seg Abr 20, 2015 16:40
- 0 Respostas
- 2366 Exibições
- Última mensagem por eulalia

Seg Abr 20, 2015 16:40
Geometria Plana
-
- Geometria Plana: área do quadrilátero inscrito
 por Celma » Sex Nov 01, 2013 10:11
por Celma » Sex Nov 01, 2013 10:11
- 2 Respostas
- 2958 Exibições
- Última mensagem por Celma

Sáb Nov 02, 2013 19:09
Geometria Plana
-
- (GEOMETRIA PLANA) Area total externa - Planificação Sólid
 por gusavancini » Qui Ago 18, 2016 12:16
por gusavancini » Qui Ago 18, 2016 12:16
- 0 Respostas
- 4080 Exibições
- Última mensagem por gusavancini

Qui Ago 18, 2016 12:16
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
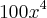 +
+



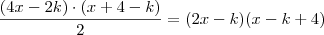 . Com o valor de
. Com o valor de  , que é este comprimento, você substitui e encontrará o outro polinômio, bastando subtrair da área total.
, que é este comprimento, você substitui e encontrará o outro polinômio, bastando subtrair da área total.

 .
. 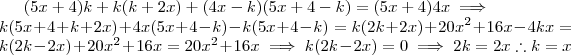 .
.  .
. ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.