Estou procurando a equação da variação da área de fechamento de uma válvula esférica em função do tempo.
*Imagem ilustrativa
Não consigo montar a equação da área de fechamento em função do tempo para calcular a área de fechamento.
Por exemplo:
Na figura a posição 1, a área fechada é 0 cm e a área aberta é de 4
 cm²
cm²Na posição 2, a parte cinza corresponde a área fechada.
O problema é calcular a área já fechada e o que me falta é a função pela variação do tempo.
O tempo médio para fechar completamente a válvula é de
 T=221ms.
T=221ms.Como faço para encontrar essa função?

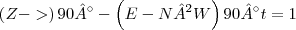




 , avisa que eu resolvo.
, avisa que eu resolvo.

