m0x0 escreveu:Começa por igualar a área do trapézio à área do triângulo, uma vez que sabes que são iguais:
O quadrilátero APQB
não é um trapézio. Note que PQ
não é paralelo a AB.
Essas conclusões são consequências de duas informações:
(i) PC = 3AP. Portanto, a razão entre PC e AC é 3/4.
(ii) A área de PQC é a metade da área de ABC. Portanto, a razão entre essas áreas é 1/2.
De (i) e (ii) segue que PQ não é paralelo a AB, pois se fossem os triângulos PQC e ABC deveriam ser semelhantes, mas isso não pode ocorrer já que a razão entre suas áreas é 1/2 e a razão entre os seus lados seria 3/4. Para que eles fossem semelhantes a razão entre seus lados nesse caso deveria ser
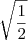
.
Joan escreveu:e os calculos que a pessoa usou:
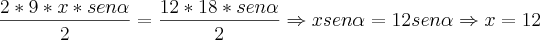
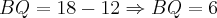
Considere a figura abaixo.

- QUESTÃO 9B.GIF (2.73 KiB) Exibido 4623 vezes
Pelos dados do exercício, sabemos que a área de PQC é a metade da área de ABC.
A área de ABC é dada por

. Mas, note que
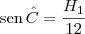
.
Por outro lado, a área de PQC é dada por

. Mas, note que

.
Como temos que
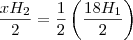
, vamos poder escrever que:



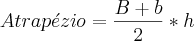
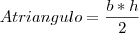
 , a menor é
, a menor é  e a altura é
e a altura é 

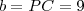 e a altura, como é um triângulo rectângulo,
e a altura, como é um triângulo rectângulo, 

 então
então 
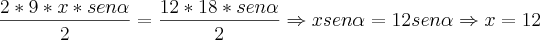
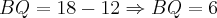
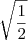 .
. . Mas, note que
. Mas, note que 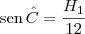 .
. . Mas, note que
. Mas, note que  .
.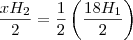 , vamos poder escrever que:
, vamos poder escrever que:

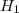 e
e 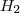 nas relações
nas relações 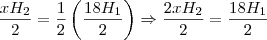
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
