 por stanley tiago » Ter Fev 15, 2011 18:24
por stanley tiago » Ter Fev 15, 2011 18:24
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Ter Fev 15, 2011 18:54
por Cleyson007 » Ter Fev 15, 2011 18:54
Olá Stanley!
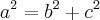
--> Teorema de Pitágoras

Outra informação:

Jogando no Teorema de Pitágoras:

Resolvendo a equação, encontra-se que o valor de c, é:
c = 5 (cateto adjacente do triângulo em questão)
Jogando o valor de c, em: [tex]a+c=11,25[tex], econtra-se:
a = 6,25 (hipotenusa do triângulo em questão).
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por stanley tiago » Ter Fev 15, 2011 21:43
por stanley tiago » Ter Fev 15, 2011 21:43
oi Cleyson007 . então agora sim deu certo o resultado .
mas da forma q vc fez nao difere muito da q eu fiz !
eu gostaria de saber aonde esta o erro, que fez com que eu nao chegasse ao resultado correto ?
agardado resposta

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Ter Fev 15, 2011 22:28
por Elcioschin » Ter Fev 15, 2011 22:28
Suas contas estão erradas
(11,25 - a)² = 126,5625 - 22,5*a + a²
3,75² = 14,0625
Continue a partir daí
Um jeito mais fácil é trabalhar com números inteiros:
a + b = 11,25 ----> a + b = 45/4 ----> b = 45/4 - a
c = 3,75 -----> c = 15/4
a² = b² + c² ----> a² = (45/4 - a)² + (15/4)² ----> a² = 45²/4² - (2*45*/4)*a + a² + 225/16
0 = 2025/16 - 90*a/4 + 225/16 ---> 90*a/4 = (2025 + 225)/16 ---> 90*a = 2250/4 ---> 9a = 225/4 ---> a = 225/36 ---> a = 6,25
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por stanley tiago » Qua Fev 16, 2011 15:16
por stanley tiago » Qua Fev 16, 2011 15:16
ah eu vi aonde esta o erro . eu esqueci de desenvolver o (quadrado da difereça )
e obrigado pela dica

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com pitagoras
por aLCANTARA » Qui Fev 25, 2010 17:22
- 3 Respostas
- 1231 Exibições
- Última mensagem por robrtoliveira

Qui Mar 25, 2010 18:27
Trigonometria
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4665 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3498 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Sáb Fev 19, 2011 10:26
- 1 Respostas
- 1921 Exibições
- Última mensagem por stanley tiago

Dom Fev 20, 2011 17:48
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12639 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



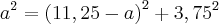
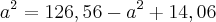

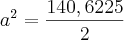
![a=\sqrt[]{70,31} a=\sqrt[]{70,31}](/latexrender/pictures/d80d48849750f2ca96e5eec4ed28e6f5.png)

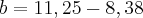
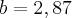


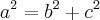 --> Teorema de Pitágoras
--> Teorema de Pitágoras





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.