 por stanley tiago » Sáb Fev 12, 2011 19:34
por stanley tiago » Sáb Fev 12, 2011 19:34
calcule a area de um triangulo retangulo , sabendo que um deuseus catetos mede o triplo do outro e que seu perimetro vale
![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png)
unidades
eu nao consegui desenvolver muita coisa desse problema . o q saiu foi isso
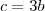


![8+2\sqrt[]{10}=3l 8+2\sqrt[]{10}=3l](/latexrender/pictures/c4893aa9250b298d2a133c42723519ae.png)
socorro!!
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por stanley tiago » Dom Fev 13, 2011 16:31
por stanley tiago » Dom Fev 13, 2011 16:31
oi amigo obrigado pela tentativa , mais eu acho q vc nao entendeu muito bem .
aqueles dados à baixo foi o que eu interpretei do problema e nao que ele tenha
nos dado no enunciado .
Infelizmente a resposta nao condiz com o gabarito q trás .......... como
6 unidade obrigado , agardo respostas

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Neperiano » Dom Fev 13, 2011 16:45
por Neperiano » Dom Fev 13, 2011 16:45
Ola
Eu nem conferi o resultado se da certo, mas acredito que de para resolver assim
Chame um cateto de x
Outro de 3x
Agora descubra a hipotenusa
h^2=x^2+(3x)^2
no final h= x+3x
Agora substitua isso no perimetro
x+3x+x+3x=8+2raiz10
Descubra o x, dai substitua ele no x e 3x, multiplique os dois e divida por dois
Acho que da certo, mas naum tenho certeza
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por stanley tiago » Dom Fev 13, 2011 18:04
por stanley tiago » Dom Fev 13, 2011 18:04
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Fuvest) Relações Métricas em Triângulos Quaisquer - Ajudem!
 por kamillanjb » Sex Jul 22, 2011 15:00
por kamillanjb » Sex Jul 22, 2011 15:00
- 1 Respostas
- 6984 Exibições
- Última mensagem por FilipeCaceres

Sex Jul 22, 2011 21:18
Geometria Plana
-
- Relaçoes metricas
 por DanielRJ » Dom Dez 18, 2011 13:22
por DanielRJ » Dom Dez 18, 2011 13:22
- 1 Respostas
- 1777 Exibições
- Última mensagem por DanielRJ

Dom Dez 18, 2011 15:33
Geometria Plana
-
- Relações Métricas
por janderson77 » Seg Dez 02, 2013 12:28
- 0 Respostas
- 941 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:28
Geometria Plana
-
- Demonstração Relações Métricas
 por PedroSantos » Ter Dez 07, 2010 22:59
por PedroSantos » Ter Dez 07, 2010 22:59
- 1 Respostas
- 1759 Exibições
- Última mensagem por VtinxD

Dom Dez 12, 2010 22:23
Trigonometria
-
- relaçoes metricas na circuferencia
 por stanley tiago » Seg Abr 11, 2011 18:37
por stanley tiago » Seg Abr 11, 2011 18:37
- 2 Respostas
- 1999 Exibições
- Última mensagem por stanley tiago

Ter Abr 12, 2011 10:06
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png) unidades
unidades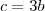


![8+2\sqrt[]{10}=3l 8+2\sqrt[]{10}=3l](/latexrender/pictures/c4893aa9250b298d2a133c42723519ae.png)

![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png) unidades
unidades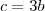


![8+2\sqrt[]{10}=3l 8+2\sqrt[]{10}=3l](/latexrender/pictures/c4893aa9250b298d2a133c42723519ae.png)

unidades

 ( Produtos dos catetos é igual o produto da hipo pela altura )
( Produtos dos catetos é igual o produto da hipo pela altura )
 ( note que a.h é o denominador da Area)
( note que a.h é o denominador da Area)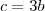
![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png)
![a+b+c=8+2\sqrt[]{10} a+b+c=8+2\sqrt[]{10}](/latexrender/pictures/dabdb8407381f1ec6a731a0cf6641ae6.png) ( substituindo )
( substituindo )![a+4b=8+2\sqrt[]{10} a+4b=8+2\sqrt[]{10}](/latexrender/pictures/45a44f06d80e9fbc5f39f03a974bbda8.png)
 ( pitagoras)
( pitagoras)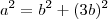
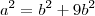

![a+4b=8+2\sqrt[]{10} a+4b=8+2\sqrt[]{10}](/latexrender/pictures/45a44f06d80e9fbc5f39f03a974bbda8.png)
![10b+4b=8+2\sqrt[]{10} 10b+4b=8+2\sqrt[]{10}](/latexrender/pictures/f699a649bd4696e96f9a62a910ae606a.png)
![14b=8+2\sqrt[]{10} 14b=8+2\sqrt[]{10}](/latexrender/pictures/63a1c021886823b05fd2e80cefdb8f9e.png)
![b=\frac{8+2\sqrt[]{10}}{14} b=\frac{8+2\sqrt[]{10}}{14}](/latexrender/pictures/75ac1faddb49d044386226f641c5b28a.png)

 ( substituindo
( substituindo  )
)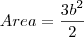
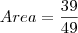




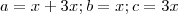
![8x=8+2\sqrt[]{10} 8x=8+2\sqrt[]{10}](/latexrender/pictures/283c1be77d69a9b982e05f293a821882.png)
![8x-8=2\sqrt[]{10} 8x-8=2\sqrt[]{10}](/latexrender/pictures/46d08ed3757cb0e7c9130c087e2e33b8.png)
![(8x-8)^2=(2\sqrt[]{10})^2 (8x-8)^2=(2\sqrt[]{10})^2](/latexrender/pictures/5bca070c05d70e60bb37d0972d7af7eb.png)
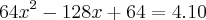
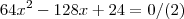
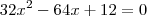


![\Delta=\sqrt[]{2560} \Delta=\sqrt[]{2560}](/latexrender/pictures/a9ce69811e9a1ab241f2c79912571430.png)
![\Delta=16\sqrt[]{10} \Delta=16\sqrt[]{10}](/latexrender/pictures/f90288326773e3bafe13aa127a1acea3.png)
![x'=\frac{4+\sqrt[]{10}}{4} x'=\frac{4+\sqrt[]{10}}{4}](/latexrender/pictures/f5b2dce8cc093a01db33c7eecbd714f8.png)
![x"=\frac{4-\sqrt[]{10}}{4} x"=\frac{4-\sqrt[]{10}}{4}](/latexrender/pictures/e559413b89cae93da6ce1a0e1fae4108.png)


 .
.
 :
: