Boa tarde estou no primeiro ano de graduação e estou tendo a materia Geometria Analitica o professor esta definindo segmento orientado e vetor. Mas para definir isso precisamos saber o que é equipolencia. Entre as definições esta tudo bem entendi bem o que sao segmentos orientados, classe de equipolência e vetores. Porem, não consigo provar e desenhar algumas coisas por exemplo:
1 - (A,B)~(C,D) IMPLICA (A,C)~(B,D) no livro em que estudo ele vez um caso particular dessa proposição no caso em que o quadrilatero ABCD é um paralelog
Após isso ele me faz tres questoes
Faça um desenho ilustrando a proposição 1 em que ABCD sao colineares.
Prove que (A,B)~(C,D) IMPLICA (B,A)~(D,C)
Prove que (A,B)~(C,D) IMPLICA (C,A)~(D,B).
Gostaria de dicas pois sei que é meio abstraro algumas coisas ainda mais quando estamos começando G.A.
Grato Flávio Santana






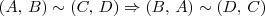

 .
.
 :
: