 por jeffersonricardo » Seg Set 06, 2010 15:20
por jeffersonricardo » Seg Set 06, 2010 15:20
plote as circunferências num mesmo sistema de eixos e passe para o papel, a região cujo ponte tem coordenadas que satisfazem o sitema de equação
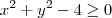
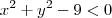
essas duas equações formam um sistema
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
 por MarceloFantini » Seg Set 06, 2010 15:23
por MarceloFantini » Seg Set 06, 2010 15:23
É a região interna ao disco de raio 3 sem a borda e externa ao disco de raio 2 incluindo a borda.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jeffersonricardo » Seg Set 06, 2010 15:25
por jeffersonricardo » Seg Set 06, 2010 15:25
não entendi
tem como mostrar com calculo
desde ja agradeço
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
 por MarceloFantini » Seg Set 06, 2010 15:35
por MarceloFantini » Seg Set 06, 2010 15:35
Não, você tem que desenhar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jeffersonricardo » Seg Set 06, 2010 17:02
por jeffersonricardo » Seg Set 06, 2010 17:02
Fantini
se tiver como olha se a resposta deste esta certa
o enunciado e o mesmo do 1

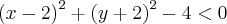
esta duas também formam um sistema
a resposta seria região interna da circunferência

sem a borda e a borda da circunferência
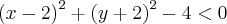
incluída sem a intersecção.
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
 por jeffersonricardo » Seg Set 06, 2010 17:02
por jeffersonricardo » Seg Set 06, 2010 17:02
Fantini
se tiver como olha se a resposta deste esta certa
o enunciado e o mesmo do 1

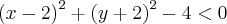
esta duas também formam um sistema
a resposta seria região interna da circunferência
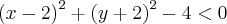
sem a borda e a borda da circunferência

incluída sem a intersecção.
Editado pela última vez por
jeffersonricardo em Seg Set 06, 2010 17:08, em um total de 2 vezes.
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
 por jeffersonricardo » Seg Set 06, 2010 17:05
por jeffersonricardo » Seg Set 06, 2010 17:05
Fantini desde ja agradeço
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
 por MarceloFantini » Seg Set 06, 2010 17:14
por MarceloFantini » Seg Set 06, 2010 17:14
Não, a resposta é a região exterior (incluindo a borda) ao disco de raio 2 e centro na origem e interna ao disco de raio 2 e centro em (2, -2), sem incluir a borda.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1875 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Circunferência
por ilovemat » Sex Abr 03, 2009 19:12
- 5 Respostas
- 9489 Exibições
- Última mensagem por Marcampucio

Seg Abr 06, 2009 20:11
Trigonometria
-
- circunferencia
 por cosme » Qua Nov 17, 2010 09:29
por cosme » Qua Nov 17, 2010 09:29
- 2 Respostas
- 1822 Exibições
- Última mensagem por MarceloFantini

Qua Nov 17, 2010 15:11
Trigonometria
-
- Circunferência
por Pri Ferreira » Qua Nov 09, 2011 21:02
- 1 Respostas
- 1304 Exibições
- Última mensagem por LuizAquino

Qui Nov 10, 2011 20:29
Funções
-
- Circunferencia
por Thays » Qui Jan 19, 2012 16:08
- 4 Respostas
- 2355 Exibições
- Última mensagem por Thays

Qui Jan 19, 2012 16:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
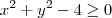
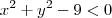

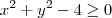
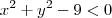






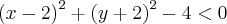
 sem a borda e a borda da circunferência
sem a borda e a borda da circunferência 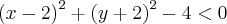 incluída sem a intersecção.
incluída sem a intersecção.

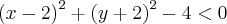
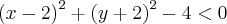 sem a borda e a borda da circunferência
sem a borda e a borda da circunferência  incluída sem a intersecção.
incluída sem a intersecção.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.