Vendo as vídeo-aulas do Luiz Aquino, especificamente esta: [http://www.youtube.com/watch?v=39f98A-rtsU]
[34. Geometria Analítica - Equação Geral das Cônicas]
Ele demonstra a equação da parábola como:

E a quação geral das cônicas como:

Ok! ...
... Mas estamos carecas de saber que a equação da parábola é
 , portanto, a equação da parábola estudada em geometria analítica não é deficiente?
, portanto, a equação da parábola estudada em geometria analítica não é deficiente? E outra, eu vi um livro que traz a equação geral das cônicas como
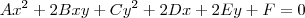 , certamente fazendo alusão ao produto notável:
, certamente fazendo alusão ao produto notável: 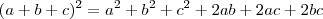 .
.E então, que me dizem? Gostaria de esclarecimentos!
Obg!


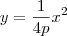 serve para representar as parábolas que possuem vértice na origem, eixo de simetria coincidindo com o eixo y e concavidade voltada para cima.
serve para representar as parábolas que possuem vértice na origem, eixo de simetria coincidindo com o eixo y e concavidade voltada para cima. , podemos efetuar translações e rotações de eixos de modo a obter a equação básica
, podemos efetuar translações e rotações de eixos de modo a obter a equação básica  (que é muito mais simples de trabalhar do que a anterior). É exatamente por isso que estudamos translações e rotações de eixos em Geometria Analítica.
(que é muito mais simples de trabalhar do que a anterior). É exatamente por isso que estudamos translações e rotações de eixos em Geometria Analítica.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.