P (1,
![\sqrt[]{14} \sqrt[]{14}](/latexrender/pictures/af2c6836f15856d3c2813ea49a068a69.png) ) e Q(2,-2
) e Q(2,-2![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) )
)Bom, tendo o eixo maior nos eixo dos y, a equação é da forma:
x²/b² + y²/a²=1
daí eu não sei tirar nada, pois pensei em substituir as coordenadas do ponto na equação , porém eu não sei a² ou b²...
resposta do livro: 2x² + y² = 16
2 - Encontrar uma equação da elipse de centro (0,0) , eixo maior sobre Ox , excentricidade 1/2 e passa pelo ponto (2,3)
Obs: Galera, realmente tentei resolver, procurar em algum lugar uma resolução pra eu entender, porém não obtive sucesso.(só pra deixar claro que não estou criando o tópico sem ao menos tentar =D)


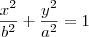



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)