 por engel » Sáb Ago 07, 2010 11:31
por engel » Sáb Ago 07, 2010 11:31
Olá!
A questão diz: " Se a é uma raiz do polinômio p(x) e b é uma raiz do polinômio q(x), então:
a)p(b)/q(a) =1
b) p(a).q(b) =1
c) p(a)+q(b) =1
d) p(b).q(a) =0
e) p(a)+q(b)=0
Bom, a sendo raiz de p, o polinômio é divisível por a. Da mesma forma b. Então, não seria alternativa B, pois sendo divisível, o produto delas resultaria em 1??? Como desenvolvo uma relação entre as raízes e os polinômios?
Obrigada pela ajuda, Abraços!!!
-
engel
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Dez 30, 2009 16:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Ago 07, 2010 14:16
por Molina » Sáb Ago 07, 2010 14:16
Boa tarde.
Você pode dar polinômios para p(x) e q(x) para ver qual o resultado que será obtido. Por exemplo, chame

e

. Assim, as raízes serão respectivamente

e

, que farão o papel de
a e
b. Mas,

e

. O que você pode concluir com isso?
Isso foi um caso particular, mas podemos generalizar para se
a é uma raiz do polinômio

e
b é uma raiz do polinômio

, então
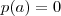
e

Acredito que poderá assinalar mais de uma alternativa...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Sáb Ago 07, 2010 16:47
por MarceloFantini » Sáb Ago 07, 2010 16:47
Como

é raíz de
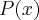
e

é raíz de

, então

e
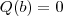
. Vamos analisar as alternativas:
a) Não conhecemos

e nem
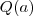
, logo não podemos afirmar que
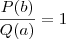
.
b)
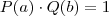
é falso, pois ambos são zero.
c) Idem pelo mesmo motivo acima.
d) Falso pelo mesmo motivo do item a.
e) Verdadeiro, pois
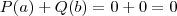
.
Molina, onde viu que haveria mais de uma alternativa?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Sáb Ago 07, 2010 16:53
por Molina » Sáb Ago 07, 2010 16:53
Fala Fantini.
Juro ter lido na alternativa d)
p(a).q(b) = 0 ao invés de
p(b).q(a) = 0 que é o que consta. Rs..

Valeu pelo toque!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polinômio] com raiz complexa
por carolsiva » Qui Jan 09, 2014 09:45
- 3 Respostas
- 3773 Exibições
- Última mensagem por anderson_wallace

Qui Jan 09, 2014 23:24
Polinômios
-
- Equação raiz e polinomio
por Rosi7 » Sáb Mai 23, 2015 09:44
- 3 Respostas
- 2739 Exibições
- Última mensagem por Rosi7

Qui Mai 28, 2015 19:33
Aritmética
-
- Integral com Raiz de polinômio no denominador
por sandermec » Qui Jul 24, 2014 02:42
- 0 Respostas
- 2735 Exibições
- Última mensagem por sandermec

Qui Jul 24, 2014 02:42
Cálculo: Limites, Derivadas e Integrais
-
- [Equação do segundo grau] Relação entre raíz e coeficiente
por Gustavo Gomes » Sex Fev 14, 2014 21:44
- 1 Respostas
- 1598 Exibições
- Última mensagem por DanielFerreira

Seg Fev 17, 2014 15:06
Equações
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7154 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e  . Assim, as raízes serão respectivamente
. Assim, as raízes serão respectivamente  e
e  , que farão o papel de
, que farão o papel de  e
e  . O que você pode concluir com isso?
. O que você pode concluir com isso? e
e  , então
, então 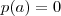 e
e 


 é raíz de
é raíz de 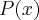 e
e  é raíz de
é raíz de  , então
, então  e
e 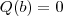 . Vamos analisar as alternativas:
. Vamos analisar as alternativas: e nem
e nem 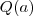 , logo não podemos afirmar que
, logo não podemos afirmar que 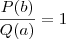 .
.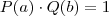 é falso, pois ambos são zero.
é falso, pois ambos são zero.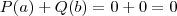 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

