Determinar respectivamente na equação:
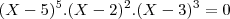
I) O grau da Equação
II) O Conjunto Verdade
a) 5 e {5,2,3}
b) 10 e {0,2,3}
c) 10 e {5,2,3}
d) 10 e {-5,-2,-3}
e) Nenhuma das Alternativas

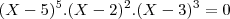

iceman escreveu:Boa tarde, gostaria que me ajudasse nessa questão abaixo, agradeceria muito pela gentileza.
Determinar respectivamente na equação:
I) O grau da Equação
II) O Conjunto Verdade
a) 5 e {5,2,3}
b) 10 e {0,2,3}
c) 10 e {5,2,3}
d) 10 e {-5,-2,-3}
e) Nenhuma das Alternativas
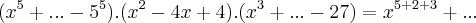
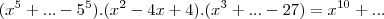

danjr5 escreveu:iceman escreveu:Boa tarde, gostaria que me ajudasse nessa questão abaixo, agradeceria muito pela gentileza.
Determinar respectivamente na equação:
I) O grau da Equação
II) O Conjunto Verdade
a) 5 e {5,2,3}
b) 10 e {0,2,3}
c) 10 e {5,2,3}
d) 10 e {-5,-2,-3}
e) Nenhuma das Alternativas
Portanto, grau 10.
As raízes são obtidas igualando as bases a zero.
x - 5 = 0
x = 5
x - 2 = 0
x = 2
x - 3 = 0
x = 3


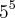 :
:  e nos outros você resolveu os expoentes?
e nos outros você resolveu os expoentes?


danjr5 escreveu:Iceman,
- Só p/ mostrar o primeiro termo do polinômio;
- É que para saber o grau do polinômio, precisamos apenas saber o grau do primeiro termo!


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)