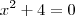
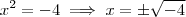 . Que como sabemos não tem solução em R.
. Que como sabemos não tem solução em R.Por outro lado, sabemos que a dita equação
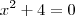 tem como solução em C, as raizes
tem como solução em C, as raizes 
A minha dúvida consiste no seguinte: ___ Como se chega aos valores das raízes complexas a partir da equação dada ?
É matemáticamente correto enunciar:
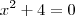
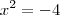
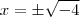

Se é correto, falta algum desenvolvimento entre o resultado final, as raízes
 e a linha imediatamente anterior
e a linha imediatamente anterior 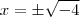 , para se chegar às ditas raízes ?
, para se chegar às ditas raízes ?Se sim, agradecia que me explicassem. Por outro lado, se não é de todo este o método de resolução, agradecia de igual modo que me explicassem a forma correta de a resolver, desde o início.
Grato
Armando




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.