Ola, estou a estudar para o exame da segunda fase de mat e preciso de ajuda com alguns exercícios.
Uma caixa contem 2 bolas pretas, uma bola verde e n bolas amarelas. Considere a seguinte experiência: ao acaso, retiram-se simultaneamente duas bolas da caixa.
Sabendo que a probabilidade de uma ser amarela e a outra verde é de 5/39, determine o valor de n.
Eles resolvem o exercício usando esta equação n/(1+n)combinações de 2 = 5/39 e o resultado da 10. Eu não entendo como é que eles chegaram à equação.


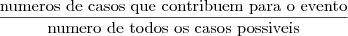

 bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de
bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de  a
a 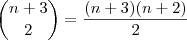

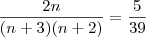 que é uma equação do segundo grau em
que é uma equação do segundo grau em  , cuja raiz natural é
, cuja raiz natural é  , de fato.
, de fato.
