 por alexpt » Sex Jul 09, 2010 08:40
por alexpt » Sex Jul 09, 2010 08:40
Ola, estou a estudar para o exame da segunda fase de mat e preciso de ajuda com alguns exercícios.
Uma caixa contem 2 bolas pretas, uma bola verde e n bolas amarelas. Considere a seguinte experiência: ao acaso, retiram-se simultaneamente duas bolas da caixa.
Sabendo que a probabilidade de uma ser amarela e a outra verde é de 5/39, determine o valor de n.
Eles resolvem o exercício usando esta equação n/(1+n)combinações de 2 = 5/39 e o resultado da 10. Eu não entendo como é que eles chegaram à equação.
-
alexpt
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 09, 2010 08:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Tom » Sex Jul 09, 2010 09:39
por Tom » Sex Jul 09, 2010 09:39
Começaremos com o cálculo da probabilidade de se retirar, simultaneamente, uma bola
amarela e uma bola
verde.
Por definição, a probabilidade pode ser entendida como:
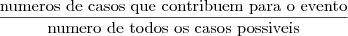
Ora, o evento
RETIRAR UMA BOLA AMARELA E UMA BOLA VERDE pode acontecer das seguintes formas:
Uma das bolas retiradas sempre é verde, e como só existe uma bola verde na caixa, então basta contar o número de bolas amarelas. Nesse caso estamos usando o conceito de combinação, já que não existe a relação de ordem, pois as bolas são retiradas simultaneamente.
Concluímos, portanto que:

Agora devemos contar de quantas maneiras distintas duas bolas podem ser retiradas: Como existem

bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de

bolas tomadas

a

, isto é:
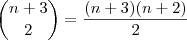
Por fim, a probabilidade de se retirar uma bola amarela e uma bola verde será:

Com efeito, fazemos:
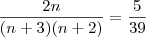
que é uma equação do segundo grau em

, cuja raiz natural é

, de fato.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por alexpt » Sex Jul 09, 2010 10:31
por alexpt » Sex Jul 09, 2010 10:31
Tom escreveu:Começaremos com o cálculo da probabilidade de se retirar, simultaneamente, uma bola
amarela e uma bola
verde.
Por definição, a probabilidade pode ser entendida como:
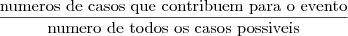
Ora, o evento
RETIRAR UMA BOLA AMARELA E UMA BOLA VERDE pode acontecer das seguintes formas:
Uma das bolas retiradas sempre é verde, e como só existe uma bola verde na caixa, então basta contar o número de bolas amarelas. Nesse caso estamos usando o conceito de combinação, já que não existe a relação de ordem, pois as bolas são retiradas simultaneamente.
Concluímos, portanto que:

Agora devemos contar de quantas maneiras distintas duas bolas podem ser retiradas: Como existem

bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de

bolas tomadas

a

, isto é:
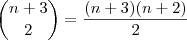
Por fim, a probabilidade de se retirar uma bola amarela e uma bola verde será:

Com efeito, fazemos:
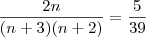
que é uma equação do segundo grau em

, cuja raiz natural é

, de fato.
Adoro-te

Obrigado pela explicação. Acho que o que me confundiu no inicio foi a bola verde que contribui para o evento não estar representada mas agora percebi porque.
-
alexpt
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 09, 2010 08:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exame Nacional
 por joaofonseca » Seg Jun 27, 2011 09:27
por joaofonseca » Seg Jun 27, 2011 09:27
- 2 Respostas
- 3603 Exibições
- Última mensagem por joaofonseca

Seg Jun 27, 2011 18:36
Educação
-
- Questões de Exame
 por joaofonseca » Qui Dez 22, 2011 21:27
por joaofonseca » Qui Dez 22, 2011 21:27
- 0 Respostas
- 1497 Exibições
- Última mensagem por joaofonseca

Qui Dez 22, 2011 21:27
Funções
-
- duvidas exame de suficiencia CRC
por dinho » Qui Mar 10, 2011 23:41
- 1 Respostas
- 3295 Exibições
- Última mensagem por Rogerio Murcila

Qui Mar 17, 2011 00:03
Matemática Financeira
-
- Exame nacional de Matemática
 por joaofonseca » Qui Jun 21, 2012 20:43
por joaofonseca » Qui Jun 21, 2012 20:43
- 10 Respostas
- 8893 Exibições
- Última mensagem por andrehp

Dom Mar 17, 2013 21:29
Vestibulares
-
- Ajuda ( Estudar para exame)
por legendkiller2009 » Qui Jun 02, 2011 09:37
- 6 Respostas
- 4023 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


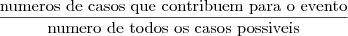

 bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de
bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de  a
a 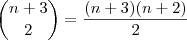

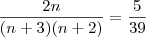 que é uma equação do segundo grau em
que é uma equação do segundo grau em  , cuja raiz natural é
, cuja raiz natural é  , de fato.
, de fato.






