 0.
0.a) Calcule de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre Luís e Antônio.
b) Calcule de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre Pedro,Luís e Antônio.
Por favor, quem for resolver me explique o porquê do ( n+1) .... que foi o q eu não entendi..
Obrigada !


 , onde
, onde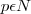 (N = conjunto dos números naturais).
(N = conjunto dos números naturais).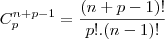
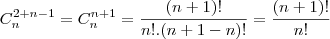
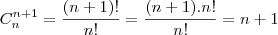

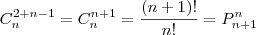
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)