380625 escreveu:Seguindo a idéia que vc começou chego na seguinte matriz
1 1 -a 0
0 1 1 -a/a-1
0 0 a^2 + a - 2 2 - 2a
Considere as seguintes operações na matriz estendida original:
Isso produz a matriz:
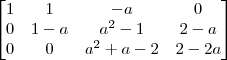
380625 escreveu:Agora o que tenho que fazer achar o valor de a, para isso usei a expressão:
a^2 + a - 2 = 0 e encontrei
a = -2 e a = 1
Na verdade, você deveria analisar duas equações:
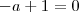
e
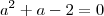
.
Mas, acontece que nesse exercício essas duas equações tem uma solução em comum (que é a = 1). Sendo assim, no final haverá apenas dois valores que zeram o determinante da matriz dos coeficientes, que seriam a = -2 e a = 1.
380625 escreveu:Discutindo o sistema temos que:
Se a = 1 ou a = -2 Sistema Imcompativel
Cuidado! Mesmo quando a matriz dos coeficientes tem determinante nulo, o sistema pode ter solução. Por exemplo, ele poderá ser compatível e indeterminado. Você precisa substituir cada um dos valores de a e verificar se isso acontece.
380625 escreveu:Se a diferente de 1 e diferente de - 2 Sistema Compativel e Determinado.
Ok.
380625 escreveu:Se a = 1 temos que a linha 3 sera constituidas de zero isso me deixa confuso.
Qual é a confusão? Se a = 1, teremos a matriz:

Observando a segunda linha, veja que o sistema é incompatível.
380625 escreveu:Desculpa mais ainda não sei usar o TEx mas ja começei ler alguns coisas sobre.
Procure fazer um esforço para aprender a digitar as matrizes usando o LaTeX. A forma como você está digitando não é adequada.
Veja que para digitar, por exemplo, uma matriz 3 por 3, basta usar o comando:
- Código: Selecionar todos
[tex]
\begin{bmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{bmatrix}
[/tex]
O resultado desse comando é:





 . Desse modo ficamos com:
. Desse modo ficamos com: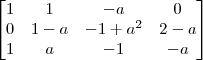


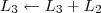
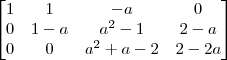
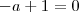 e
e 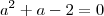 .
.
