Como aplicar o metodo de Gauss Jordan nesse sistema.

por **380625** » Sáb Ago 20, 2011 16:19

Como aplicar o metodo de gauss jordan no seguinte exercicio:

Discutir os seguintes sistemas lineares ( em função de a):

x + y - az = 0 ax + 2y = 6
ax + y - z = 2 - a e 3x - y = -2
x + ay - z = -a x + y = 0

não consigo escalonar a matriz quando ela esta nesse modelo.

Obrigado
Flávio Santana.

por **LuizAquino** » Dom Ago 28, 2011 00:50

Por favor, use o LaTeX para digitar os sistemas.

Por exemplo, o comando LaTeX abaixo cria o primeiro sistema:

Código: Selecionar todos: [tex] \begin{cases} x + y - az = 0 \\ ax + y - z = 2 - a \\ x + ay - z = -a \end{cases} [/tex]

O resultado do comando é:
$\begin{cases} x + y - az = 0 \\ ax + y - z = 2 - a \\ x + ay - z = -a \end{cases}$

380625 escreveu:não consigo escalonar a matriz quando ela esta nesse modelo.

Qual é exatamente a sua dúvida?

A matriz estendida do sistema é:
$\begin{bmatrix} 1 & 1 & - a & 0 \\ a & 1 & - 1 & 2 - a \\ 1 & a & -1 & -a \end{bmatrix}$

Para zerarmos, por exemplo, o termo a que aparece na segunda linha e primeira coluna, basta fazer a operação $L_2 \leftarrow L_2 - aL_1$ . Desse modo ficamos com:
$\begin{bmatrix} 1 & 1 & - a & 0 \\ 0 & 1-a & - 1 + a^2 & 2 - a \\ 1 & a & -1 & -a \end{bmatrix}$

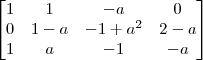
Agora basta continuar com essa ideia.

por **380625** » Dom Ago 28, 2011 15:01

Seguindo a idéia que vc começou chego na seguinte matriz

1 1 -a 0

0 1 1 -a/a-1

0 0 a^2 + a - 2 2 - 2a

Agora o que tenho que fazer achar o valor de a, para isso usei a expressão:

a^2 + a - 2 = 0 e encontrei

a = -2 e a = 1

Discutindo o sistema temos que:

Se a = 1 ou a = -2 Sistema Imcompativel

Se a diferente de 1 e diferente de - 2 Sistema Compativel e Determinado.

Esta correto a minha informação.

Pq tenho uma duvida.

Se a = 1 temos que a linha 3 sera constituidas de zero isso me deixa confuso.

Ficaria grato com a ajuda. Desculpa mais ainda não sei usar o TEx mas ja começei ler alguns coisas sobre.

Flávio Santana.

por **LuizAquino** » Dom Ago 28, 2011 22:26

380625 escreveu:Seguindo a idéia que vc começou chego na seguinte matriz

1 1 -a 0

0 1 1 -a/a-1

0 0 a^2 + a - 2 2 - 2a

Considere as seguintes operações na matriz estendida original:

$L_2 \leftarrow L_2 - aL_1$
$L_3 \leftarrow L_3 - L_1$
$L_3 \leftarrow L_3 + L_2$

Isso produz a matriz:
$\begin{bmatrix} 1 & 1 & -a & 0 \\ 0 & 1 - a & a^2 - 1 & 2 - a \\ 0 & 0 & a^2 + a - 2 & 2 - 2a \end{bmatrix}$

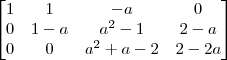
380625 escreveu:Agora o que tenho que fazer achar o valor de a, para isso usei a expressão:

a^2 + a - 2 = 0 e encontrei

a = -2 e a = 1

Na verdade, você deveria analisar duas equações: -a + 1 = 0

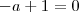
e

.

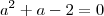
Mas, acontece que nesse exercício essas duas equações tem uma solução em comum (que é a = 1). Sendo assim, no final haverá apenas dois valores que zeram o determinante da matriz dos coeficientes, que seriam a = -2 e a = 1.

380625 escreveu:Discutindo o sistema temos que:

Se a = 1 ou a = -2 Sistema Imcompativel

Cuidado! Mesmo quando a matriz dos coeficientes tem determinante nulo, o sistema pode ter solução. Por exemplo, ele poderá ser compatível e indeterminado. Você precisa substituir cada um dos valores de a e verificar se isso acontece.

380625 escreveu:Se a diferente de 1 e diferente de - 2 Sistema Compativel e Determinado.

Ok.

380625 escreveu:Se a = 1 temos que a linha 3 sera constituidas de zero isso me deixa confuso.

Qual é a confusão? Se a = 1, teremos a matriz:
$\begin{bmatrix} 1 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}$

Observando a segunda linha, veja que o sistema é incompatível.

380625 escreveu:Desculpa mais ainda não sei usar o TEx mas ja começei ler alguns coisas sobre.

Procure fazer um esforço para aprender a digitar as matrizes usando o LaTeX. A forma como você está digitando não é adequada.

Veja que para digitar, por exemplo, uma matriz 3 por 3, basta usar o comando:

Código: Selecionar todos: [tex] \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} [/tex]

O resultado desse comando é:
$\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$

Como aplicar o metodo de Gauss Jordan nesse sistema.

Como aplicar o metodo de Gauss Jordan nesse sistema.

Como aplicar o metodo de Gauss Jordan nesse sistema.

Re: Como aplicar o metodo de Gauss Jordan nesse sistema.

Re: Como aplicar o metodo de Gauss Jordan nesse sistema.

Re: Como aplicar o metodo de Gauss Jordan nesse sistema.

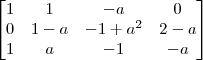
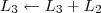
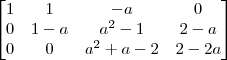
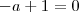Quem está online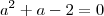