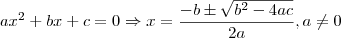por jvpetrucci » Qui Mai 03, 2012 19:14
por jvpetrucci » Qui Mai 03, 2012 19:14
[/tex]A questão é a seguinte
Por um jantar para um grupo de amigos, um restaurante cobrou R$ 240,00, mas quatro dessas pessoas não tinha dinheiro para contribuir com a despesa.
Essa atitude obrigou cada uma das demais pessoas a pagar R$ 5,00 além da parte que lhe caberia se todos participassem da divisão da conta.
Quantos eram os amigos?
Por favor me ajudem vale um ponto.
Não é uma questão simples por que aqui em meu livro ela tem 18 linhas para fazer a conta.
Eu fiz assim, não sei se ta certo
x=nº de amigos
![\frac{240}{x-4}=\frac{240}{x+5}
240x=240x-960+5x²-20x
5x²-20x-960=0
x²-4x-192=0
x= 4+-\sqrt[2]{16}+ \frac{768}{2}
x= 4+-\frac{28}{2}
x= 4+\frac{28}{2} = \frac{32}{2}=16 \frac{240}{x-4}=\frac{240}{x+5}
240x=240x-960+5x²-20x
5x²-20x-960=0
x²-4x-192=0
x= 4+-\sqrt[2]{16}+ \frac{768}{2}
x= 4+-\frac{28}{2}
x= 4+\frac{28}{2} = \frac{32}{2}=16](/latexrender/pictures/e7b2c0afcecb1fb08c2865e5034fdfe6.png)
Esse "²" deve ser pra elevar pq eu nao coloquei isso espero q vcs entendam minha forma de fazer
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por Russman » Qui Mai 03, 2012 20:35
por Russman » Qui Mai 03, 2012 20:35
Seja o número de amigos

.
Se todos os amigos pagassem então o valor

que cada um teria de pagar é calculado por
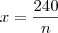
.
Porém, somente

amigos pagaram. Então, os

amigos pagaram um valor

cada dado por
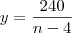
.
Do problema identificamos que
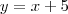
. Portanto,
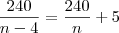
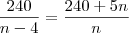
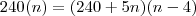
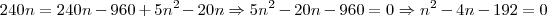
.
Esta equação tem como solução
![x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right. x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right.](/latexrender/pictures/b8975046d497897455e8ddfe487a8618.png)
.
Como só nos interessa a solução positiva, o número de amigos eram então

.
Veja que
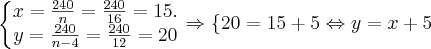
, como se era esperado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jvpetrucci » Qui Mai 03, 2012 20:48
por jvpetrucci » Qui Mai 03, 2012 20:48
Russman escreveu:Seja o número de amigos

.
Se todos os amigos pagassem então o valor

que cada um teria de pagar é calculado por
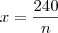
.
Porém, somente

amigos pagaram. Então, os

amigos pagaram um valor

cada dado por
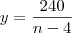
.
Do problema identificamos que
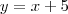
. Portanto,
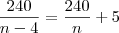
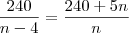
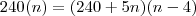
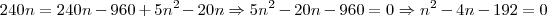
.
Esta equação tem como solução
![x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right. x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right.](/latexrender/pictures/b8975046d497897455e8ddfe487a8618.png)
.
Como só nos interessa a solução positiva, o número de amigos eram então

.
Veja que
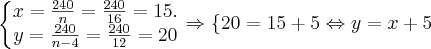
, como se era esperado.
Muito obrigado, nossa eu to doido pra ganha esse 1 ponto, porque la na sala eu sou o primeiro da turma ai tem que tira nota boa e consegui os pontos
Alem de que eu no bimestre passado nao fui muito bem nas provas.
Eu só não to conseguindo entender essa parte aqui
Esta equação tem como solução
![x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right. x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right.](/latexrender/pictures/b8975046d497897455e8ddfe487a8618.png)
.
Como só nos interessa a solução positiva, o número de amigos eram então

de onde vc tiro esse 28 dessa raiz?
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por Russman » Qui Mai 03, 2012 21:15
por Russman » Qui Mai 03, 2012 21:15
Veja que
![\sqrt[]{16 + 4.192} = \sqrt[]{784} = 28 \sqrt[]{16 + 4.192} = \sqrt[]{784} = 28](/latexrender/pictures/b27a894e743fca749970a4f816038a95.png)
.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jvpetrucci » Qui Mai 03, 2012 21:23
por jvpetrucci » Qui Mai 03, 2012 21:23
Russman escreveu:Veja que
![\sqrt[]{16 + 4.192} = \sqrt[]{784} = 28 \sqrt[]{16 + 4.192} = \sqrt[]{784} = 28](/latexrender/pictures/b27a894e743fca749970a4f816038a95.png)
.
(:
O q vc fez?
e pq eu to tentando fazer mas nao to conseguindo
vc tiro a raiz de um e de outro?
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por Russman » Qui Mai 03, 2012 21:26
por Russman » Qui Mai 03, 2012 21:26
Nãao!
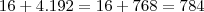
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jvpetrucci » Qui Mai 03, 2012 21:30
por jvpetrucci » Qui Mai 03, 2012 21:30
Russman escreveu:Nãao!
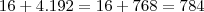
Ai não entendi de onde vc tiro o 768
Eu quero sabe se vc fatoro oq vc fez?
pq vc bota desse jeito ai eu fico sem entender
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por jvpetrucci » Qui Mai 03, 2012 21:31
por jvpetrucci » Qui Mai 03, 2012 21:31
Russman escreveu:Nãao!
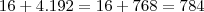
e o 784 nao entendi como vc fez
Eu queria q vc explicasse q processo vc uso
pq alem de estar fazer o exercicio eu estou estudando ja para o teste e prova
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por Russman » Qui Mai 03, 2012 21:42
por Russman » Qui Mai 03, 2012 21:42
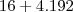
Isto é

somado com

vezes
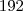
.
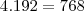
.
Eu usei a fórmula da solução da equação de 2° grau! Você deve conhecer.
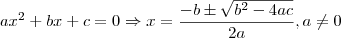
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jvpetrucci » Qui Mai 03, 2012 21:43
por jvpetrucci » Qui Mai 03, 2012 21:43
Russman escreveu: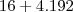
Isto é

somado com

vezes
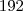
.
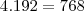
.
Eu usei a fórmula da solução da equação de 2° grau! Você deve conhecer.
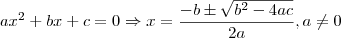
Ata vc usou o processo de baskaras nao foi?
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por Russman » Qui Mai 03, 2012 21:59
por Russman » Qui Mai 03, 2012 21:59
Isto, isto!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jvpetrucci » Qui Mai 03, 2012 22:00
por jvpetrucci » Qui Mai 03, 2012 22:00
Obrigado por ter me ajudado e explicado essa questão
-
jvpetrucci
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 03, 2012 18:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Informática, montagem e manutenção
- Andamento: formado
 por Russman » Qui Mai 03, 2012 22:35
por Russman » Qui Mai 03, 2012 22:35
Não por isso. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Problemas de Equaçoes]
por R0nny » Sáb Mai 04, 2013 15:01
- 2 Respostas
- 3456 Exibições
- Última mensagem por R0nny

Sáb Mai 04, 2013 19:51
Equações
-
- problemas com equacoes de 1 grau
por luanxd » Qua Jan 27, 2010 23:14
- 2 Respostas
- 2337 Exibições
- Última mensagem por luanxd

Sáb Jan 30, 2010 23:31
Polinômios
-
- Problemas com equações biquadradas
por Viivii » Qua Ago 24, 2011 23:05
- 4 Respostas
- 4030 Exibições
- Última mensagem por Neperiano

Qui Ago 25, 2011 17:59
Sistemas de Equações
-
- Problemas matemáticos envolvendo equações.
por mynameisnandoo » Qui Out 06, 2011 14:57
- 0 Respostas
- 2647 Exibições
- Última mensagem por mynameisnandoo

Qui Out 06, 2011 14:57
Tópicos sem Interação (leia as regras)
-
- [Problemas de Valor Inicial] Equações Diferenciais
por mayconf » Ter Abr 15, 2014 18:24
- 1 Respostas
- 2110 Exibições
- Última mensagem por Russman

Ter Abr 15, 2014 22:28
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{240}{x-4}=\frac{240}{x+5}
240x=240x-960+5x²-20x
5x²-20x-960=0
x²-4x-192=0
x= 4+-\sqrt[2]{16}+ \frac{768}{2}
x= 4+-\frac{28}{2}
x= 4+\frac{28}{2} = \frac{32}{2}=16 \frac{240}{x-4}=\frac{240}{x+5}
240x=240x-960+5x²-20x
5x²-20x-960=0
x²-4x-192=0
x= 4+-\sqrt[2]{16}+ \frac{768}{2}
x= 4+-\frac{28}{2}
x= 4+\frac{28}{2} = \frac{32}{2}=16](/latexrender/pictures/e7b2c0afcecb1fb08c2865e5034fdfe6.png)


 .
. que cada um teria de pagar é calculado por
que cada um teria de pagar é calculado por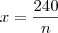 .
. amigos pagaram. Então, os
amigos pagaram. Então, os  cada dado por
cada dado por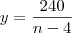 .
.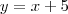 . Portanto,
. Portanto,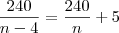
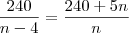
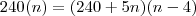
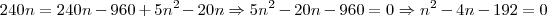 .
.![x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right. x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right.](/latexrender/pictures/b8975046d497897455e8ddfe487a8618.png) .
. .
.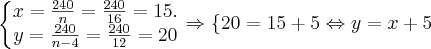 , como se era esperado.
, como se era esperado.
![\sqrt[]{16 + 4.192} = \sqrt[]{784} = 28 \sqrt[]{16 + 4.192} = \sqrt[]{784} = 28](/latexrender/pictures/b27a894e743fca749970a4f816038a95.png) .
.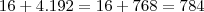
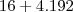
 somado com
somado com  vezes
vezes 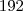 .
.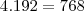 .
.