Por um jantar para um grupo de amigos, um restaurante cobrou R$ 240,00, mas quatro dessas pessoas não tinha dinheiro para contribuir com a despesa.
Essa atitude obrigou cada uma das demais pessoas a pagar R$ 5,00 além da parte que lhe caberia se todos participassem da divisão da conta.
Quantos eram os amigos?
Por favor me ajudem vale um ponto.
Não é uma questão simples por que aqui em meu livro ela tem 18 linhas para fazer a conta.
Eu fiz assim, não sei se ta certo
x=nº de amigos
![\frac{240}{x-4}=\frac{240}{x+5}
240x=240x-960+5x²-20x
5x²-20x-960=0
x²-4x-192=0
x= 4+-\sqrt[2]{16}+ \frac{768}{2}
x= 4+-\frac{28}{2}
x= 4+\frac{28}{2} = \frac{32}{2}=16 \frac{240}{x-4}=\frac{240}{x+5}
240x=240x-960+5x²-20x
5x²-20x-960=0
x²-4x-192=0
x= 4+-\sqrt[2]{16}+ \frac{768}{2}
x= 4+-\frac{28}{2}
x= 4+\frac{28}{2} = \frac{32}{2}=16](/latexrender/pictures/e7b2c0afcecb1fb08c2865e5034fdfe6.png)
Esse "²" deve ser pra elevar pq eu nao coloquei isso espero q vcs entendam minha forma de fazer


 .
. que cada um teria de pagar é calculado por
que cada um teria de pagar é calculado por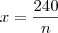 .
. amigos pagaram. Então, os
amigos pagaram. Então, os  cada dado por
cada dado por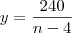 .
.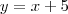 . Portanto,
. Portanto,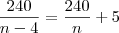
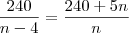
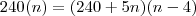
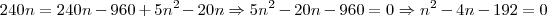 .
.![x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right. x = \frac{4+-\sqrt[]{16+4.192}}{2} = \left\{\begin{matrix}
x_{1} = \frac{4+28}{2} = 16\\
x_{2} = \frac{4-28}{2} = -12
\end{matrix}\right.](/latexrender/pictures/b8975046d497897455e8ddfe487a8618.png) .
. .
.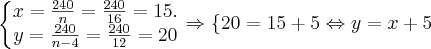 , como se era esperado.
, como se era esperado.
![\sqrt[]{16 + 4.192} = \sqrt[]{784} = 28 \sqrt[]{16 + 4.192} = \sqrt[]{784} = 28](/latexrender/pictures/b27a894e743fca749970a4f816038a95.png) .
.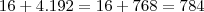
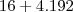
 somado com
somado com  vezes
vezes 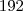 .
.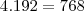 .
.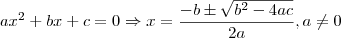
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)