por Abner » Sex Mai 20, 2011 17:36
.resolva o sistema de equações lineares
(8 -5 2 ) ( x ) 0
3 -1 1 . y = 0
1 2 1 z 0
e discuta o significado geometrico se existir
-
Abner
- Usuário Parceiro
-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por Molina » Sex Mai 20, 2011 19:08
Boa tarde, Abner.
Procure utilizar a linguagem LaTeX para postar expressões matemáticas.
Confirme se é isso:
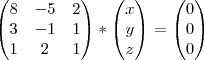
Fico no aguardo,
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
por lanca » Sáb Mai 21, 2011 15:26
Oi Abner...
Fiz por escalonamento mas ainda não consegui entender a forma geométrica
-
lanca
- Usuário Ativo
-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
por lanca » Sáb Mai 21, 2011 15:27
Oi Molina!!
A expressão é essa mesma.
-
lanca
- Usuário Ativo
-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
por Abner » Sáb Mai 21, 2011 16:25
Molina desculpe não saber usar o Latex mas é isso mesmo....
-
Abner
- Usuário Parceiro
-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por lanca » Sáb Mai 21, 2011 20:10
Oi Abner...
Fiz por escalonamento e cheguei nesse resultado,ve se confere com o seu..
y=-2z/7 e x= -1z/14
fiz em função de z
-
lanca
- Usuário Ativo
-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
por lanca » Sáb Mai 21, 2011 22:54
Oi Abner...
Refiz meus cálculos...por escalonamento vamos ter;
y= -2z/7 e x= -3z/7
Estou concluindo a forma algébrica
-
lanca
- Usuário Ativo
-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
por LuizAquino » Dom Mai 22, 2011 19:10
Exercício já resolvido na mensagem:
Re: Sistema linear por matrizviewtopic.php?p=16213#p16213
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas Lineares
por Cleyson007 » Sáb Mai 03, 2008 01:50
- 3 Respostas
- 7040 Exibições
- Última mensagem por admin
Dom Mai 04, 2008 13:51
Sistemas de Equações
-
- Sistemas Lineares
por gustavowelp » Sáb Jun 26, 2010 17:05
- 3 Respostas
- 7801 Exibições
- Última mensagem por Douglasm
Dom Jun 27, 2010 09:09
Sistemas de Equações
-
- Sistemas lineares
por Catriane Moreira » Seg Set 06, 2010 18:32
- 1 Respostas
- 2492 Exibições
- Última mensagem por Molina
Seg Set 06, 2010 19:13
Sistemas de Equações
-
- sistemas lineares
por angeloka » Sáb Nov 27, 2010 17:59
- 1 Respostas
- 2635 Exibições
- Última mensagem por Neperiano
Sáb Nov 27, 2010 19:02
Sistemas de Equações
-
- sistemas lineares
por angeloka » Sáb Nov 27, 2010 22:10
- 0 Respostas
- 1817 Exibições
- Última mensagem por angeloka
Sáb Nov 27, 2010 22:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
