 .
.  =
= 
e discuta o significado geométrico do conjunto solução, se exixtir.

 .
.  =
= 

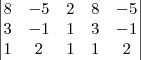
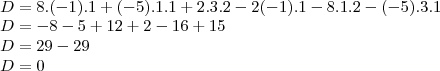
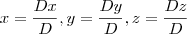

 , já temos uma solução. Neste caso, o sistema é possível e indeterminado, pois existem inúmeras soluções.
, já temos uma solução. Neste caso, o sistema é possível e indeterminado, pois existem inúmeras soluções.




 é a equação de um plano, logo, se a única solução é a trivial, isso quer dizer três planos que se interceptam apenas na origem. Outras possibilidades são: três planos que tem uma reta em comum ou na verdade são o mesmo plano.
é a equação de um plano, logo, se a única solução é a trivial, isso quer dizer três planos que se interceptam apenas na origem. Outras possibilidades são: três planos que tem uma reta em comum ou na verdade são o mesmo plano.







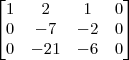
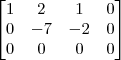


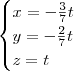

Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
