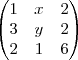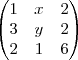por angela sofia Pereira » Sáb Nov 12, 2011 11:39
por angela sofia Pereira » Sáb Nov 12, 2011 11:39
considerando a seguinte matriz pede-se para calcular o determinante da matriz como função de x e y por expansão de Laplace, explicitando os pontos x e y para os quais a matriz é invertivel. Já tentei resolver de várias formas mas não chego a nenhuma conclusão, pedia um pequeno auxilio para solucionar esta questão.
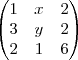
-
angela sofia Pereira
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Nov 12, 2011 10:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: matemática
- Andamento: cursando
 por LuizAquino » Sáb Nov 12, 2011 12:27
por LuizAquino » Sáb Nov 12, 2011 12:27
angela sofia Pereira escreveu:considerando a seguinte matriz pede-se para calcular o determinante da matriz como função de x e y por expansão de Laplace, explicitando os pontos x e y para os quais a matriz é invertivel. Já tentei resolver de várias formas mas não chego a nenhuma conclusão, pedia um pequeno auxilio para solucionar esta questão.
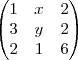
Por favor, envie a sua resolução para que possamos identificar o erro.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por angela sofia Pereira » Sáb Nov 12, 2011 15:17
por angela sofia Pereira » Sáb Nov 12, 2011 15:17
LuizAquino escreveu:angela sofia Pereira escreveu:considerando a seguinte matriz pede-se para calcular o determinante da matriz como função de x e y por expansão de Laplace, explicitando os pontos x e y para os quais a matriz é invertivel. Já tentei resolver de várias formas mas não chego a nenhuma conclusão, pedia um pequeno auxilio para solucionar esta questão.
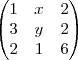
Por favor, envie a sua resolução para que possamos identificar o erro.
boa tarde, a minha duvida é se o que é pedido é apenas o determinante desta matriz que já calculei e dava 2y-14x+4 ou se em primeiro lugar tenho de achar as variáveis x e y de n sei como fazer, no manual não encontro nada que se assemelhe ou então não estou mesmo a perceber, visualizei em outros sitios e existia uma forma de calcular as variáveis apartir da transpota ou seja a matriz x se esta fosse simétrica seria igual á sua transposta e ficaria com x= 3 e y= 0 mas os valores da matriz teriam de ser identicos à transposta, e não me dá isso, e tentei pela forma antisimétrica e tambem os valores não são idênticos, e fiquei nesse impasse, pelo o que penso eu tenho de saber primeiro os valores de x e y só não estou a ver como faze-lo. Não saberei se esta matriz é invertivel se não tiver o valor do determinante que terá de ser diferente de zero. Porque a pergunta b tambem refere diversos valores para x e y e pede para justificar em qual deles é invertivel e após as diversas contas não me dá menhum valor igual ao pretendido, peço desculpa desde já de não colocar aqui todas as contas e são muitas mas a minha prática em latex é muito pouca e levaria muito tempo.se esta matriz não tivesse as váriáveis o resto eu sei fazer, mas realmente bloquiei nesta parte. Agradeço desde já a vossa disponibilidade e muito boa tarde, Cumprimentos
-
angela sofia Pereira
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Nov 12, 2011 10:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: matemática
- Andamento: cursando
 por LuizAquino » Sáb Nov 12, 2011 19:06
por LuizAquino » Sáb Nov 12, 2011 19:06
angela sofia Pereira escreveu:(...) a minha duvida é se o que é pedido é apenas o determinante desta matriz que já calculei e dava 2y-14x+4 ou se em primeiro lugar tenho de achar as variáveis x e y de n sei como fazer (...)
Na primeira parte do enunciado do exercício está escrito: "
considerando a seguinte matriz pede-se para calcular o determinante da matriz como função de x e y por expansão de Laplace (...)"
Portanto, primeiro pede-se para calcular o determinante por expansão de Laplace. Nesse caso, você irá obter:

Já na segunda parte do enunciado do exercício está escrito: "(...)
explicitando os pontos x e y para os quais a matriz é invertível. (...)"
Portanto, em segundo lugar pede-se para determinar que pontos (x, y) tornam a matriz inversível.
Para possuir inversa, o determinante dessa matriz deve ser diferente de zero. Ou seja, deve ocorrer:

Nesse caso, os pontos (x, y) para os quais a matriz possui inversa estão no conjunto:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por angela sofia Pereira » Sáb Nov 12, 2011 21:48
por angela sofia Pereira » Sáb Nov 12, 2011 21:48
boa noite, agradeço imenso a ajuda prestada agora já percebi o que era pedido.
Cumprimentos
Ângela Pereira
-
angela sofia Pereira
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Nov 12, 2011 10:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: matemática
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- 328 Matrizes e Determinantes
por Colton » Qui Out 28, 2010 17:57
- 2 Respostas
- 2198 Exibições
- Última mensagem por Colton

Sex Out 29, 2010 08:37
Matrizes e Determinantes
-
- [Matrizes e Determinantes]
por 47elizeu » Qui Set 04, 2014 19:05
- 1 Respostas
- 4600 Exibições
- Última mensagem por 47elizeu

Sáb Set 06, 2014 21:22
Matrizes e Determinantes
-
- [Determinantes] Inversão de Matrizes
 por vanessafey » Sex Set 02, 2011 22:52
por vanessafey » Sex Set 02, 2011 22:52
- 5 Respostas
- 3755 Exibições
- Última mensagem por vanessafey

Sáb Set 03, 2011 16:35
Matrizes e Determinantes
-
- determinantes - matrizes envolvendo trigonometria
por natanaelskt » Sex Abr 26, 2013 10:23
- 1 Respostas
- 2999 Exibições
- Última mensagem por DanielFerreira

Sex Abr 26, 2013 21:48
Matrizes e Determinantes
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5156 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.