 por JKS » Qui Abr 11, 2013 01:24
por JKS » Qui Abr 11, 2013 01:24
preciso de ajuda,desde já agradeço!
Ache o valor do 25° termo da pg alternante e infinita, sabendo que q =
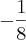
e S=
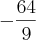
.
GABARITO :

-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Ter Abr 16, 2013 12:15
por DanielFerreira » Ter Abr 16, 2013 12:15
Jks,
bom dia!
Procure expor suas tentativas ao resolver as questões. Fica mais fácil identificar onde 'reside' a dúvida; ou, apenas a resolução é suficiente?
Segue,
Determinemos o primeiro termo da sequência da seguinte forma:

Agora podemos achar o 25° termo.

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por JKS » Dom Abr 21, 2013 18:16
por JKS » Dom Abr 21, 2013 18:16
Muito Obrigada , vou tentar expor minhas tentativas, é porque na resolução das questões feitas por vocês, na maioria das vezes,eu consigo identificar onde foi meu erro,mas quando eu não conseguir eu publico aqui ,mais uma vez te agradeço por me ajudar !!
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sex Abr 26, 2013 21:30
por DanielFerreira » Sex Abr 26, 2013 21:30
Então tá!

Até a próxima!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequência alternante PG e PA]
por JKS » Qui Abr 11, 2013 01:45
- 0 Respostas
- 1134 Exibições
- Última mensagem por JKS

Qui Abr 11, 2013 01:45
Progressões
-
- Soma de uma PG infinita
por silvia fillet » Qua Fev 15, 2012 19:53
- 12 Respostas
- 9023 Exibições
- Última mensagem por Rosana Vieira

Qua Fev 22, 2012 17:44
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 2090 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:52
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 1881 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:49
Progressões
-
- [PG infinita com trigonometria] ITA-SP
por JKS » Qui Abr 11, 2013 01:54
- 1 Respostas
- 2386 Exibições
- Última mensagem por e8group

Qui Abr 11, 2013 13:27
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
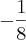 e S=
e S= 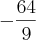 .
.

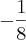 e S=
e S= 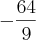 .
.







