Na figura, I é o incentro do triângulo ABC. Sabendo que
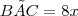 e
e  , determine x.
, determine x.Tentei resolver dessa forma!
Observando a bissetriz B1 com a bissetriz C1, forma um angulo reto, de 90 graus. Então fiz os cálculos abaixo:

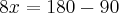

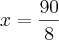
x = 11 graus e 15 minutos
Mas a resposta no livro é x = 12 graus.
Não estou entendendo.






 .
.
 :
: