 por LuizCarlos » Dom Abr 01, 2012 19:00
por LuizCarlos » Dom Abr 01, 2012 19:00
Estou tentando resolver uma questão, mas o resultado que obtive, não é a mesma da resposta do livro!
Na figura, I é o incentro do triângulo ABC. Sabendo que
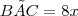
e

, determine x.
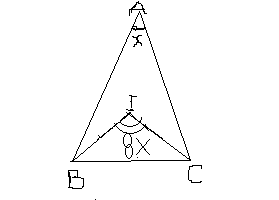
- Triângulo_incentro.png (3.19 KiB) Exibido 7422 vezes
Tentei resolver dessa forma!
Observando a bissetriz B1 com a bissetriz C1, forma um angulo reto, de 90 graus. Então fiz os cálculos abaixo:
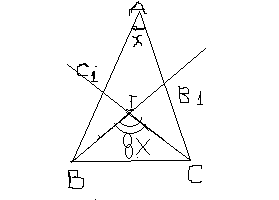
- Triângulo_incentro2.png (3.53 KiB) Exibido 7422 vezes

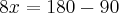

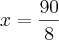
x = 11 graus e 15 minutos
Mas a resposta no livro é x = 12 graus.
Não estou entendendo.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Pedro123 » Dom Abr 01, 2012 19:30
por Pedro123 » Dom Abr 01, 2012 19:30
Bom cara, o problema todo da questão, é que você nao pode afirmar com certeza que o angulo entre a bissetriz e o lado do triângulo é exatamente 90º, so se pode afirmar isso se o triângulo for equilátero ou isósceles (apenas no lado que é diferente dos 2).
Mas vamos à resolução.
Considerando o triângulo ABC, temos a condição angular :
X + B + C = 180 --> B + C = 180 - X . Porém, no triangulo BCI:
8X + B/2 + C/2 = 180 --> 16x + B + C = 360.
substituindo uma na outra :
16x + 180 - x = 360
15 x = 180
x = 12º.
qualquer duvida estamos ai
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por NMiguel » Dom Abr 01, 2012 19:46
por NMiguel » Dom Abr 01, 2012 19:46
LuizCarlos escreveu:Tentei resolver dessa forma!
Observando a bissetriz B1 com a bissetriz C1, forma um angulo reto, de 90 graus. Então fiz os cálculos abaixo:

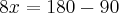

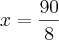
x = 11 graus e 15 minutos
Mas a resposta no livro é x = 12 graus.
Não estou entendendo.
O teu erro neste raciocínio foi supores que o ângulo formado pelas duas bissetrizes é reto. Isso não acontece. Daí teres obtido um resultado errado.
-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
 por LuizCarlos » Dom Abr 01, 2012 20:48
por LuizCarlos » Dom Abr 01, 2012 20:48
Pedro123 escreveu:Bom cara, o problema todo da questão, é que você nao pode afirmar com certeza que o angulo entre a bissetriz e o lado do triângulo é exatamente 90º, so se pode afirmar isso se o triângulo for equilátero ou isósceles (apenas no lado que é diferente dos 2).
Mas vamos à resolução.
Considerando o triângulo ABC, temos a condição angular :
X + B + C = 180 --> B + C = 180 - X . Porém, no triangulo BCI:
8X + B/2 + C/2 = 180 --> 16x + B + C = 360.
substituindo uma na outra :
16x + 180 - x = 360
15 x = 180
x = 12º.
qualquer duvida estamos ai
Obrigado Pedro123, entendi agora, vacilei feio!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Dom Abr 01, 2012 20:49
por LuizCarlos » Dom Abr 01, 2012 20:49
NMiguel escreveu:LuizCarlos escreveu:Tentei resolver dessa forma!
Observando a bissetriz B1 com a bissetriz C1, forma um angulo reto, de 90 graus. Então fiz os cálculos abaixo:

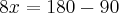

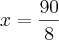
x = 11 graus e 15 minutos
Mas a resposta no livro é x = 12 graus.
Não estou entendendo.
O teu erro neste raciocínio foi supores que o ângulo formado pelas duas bissetrizes é reto. Isso não acontece. Daí teres obtido um resultado errado.
È verdade NMiguel, vacilei! mas agora entendi.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema com triângulo incentro
 por Vinicius das duvidas » Ter Jul 14, 2015 21:57
por Vinicius das duvidas » Ter Jul 14, 2015 21:57
- 0 Respostas
- 2358 Exibições
- Última mensagem por Vinicius das duvidas

Ter Jul 14, 2015 21:57
Geometria Plana
-
- [Trigonometria] Dúvida... questão sobre triangulo retangulo
 por rochadapesada » Qua Abr 24, 2013 17:57
por rochadapesada » Qua Abr 24, 2013 17:57
- 5 Respostas
- 3226 Exibições
- Última mensagem por young_jedi

Qui Abr 25, 2013 23:26
Trigonometria
-
- Explicação sobre triângulo inscrito em circunferência
por tom_junior » Ter Jun 30, 2009 23:31
- 1 Respostas
- 5251 Exibições
- Última mensagem por Marcampucio

Qua Jul 01, 2009 14:47
Geometria Plana
-
- Incentro
 por Analt » Sex Mai 06, 2011 15:36
por Analt » Sex Mai 06, 2011 15:36
- 2 Respostas
- 3048 Exibições
- Última mensagem por Analt

Dom Mai 08, 2011 15:23
Geometria Plana
-
- incentro
por davipepe » Seg Ago 20, 2012 13:11
- 2 Respostas
- 1861 Exibições
- Última mensagem por davipepe

Seg Ago 20, 2012 23:53
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
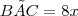 e
e  , determine x.
, determine x.
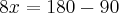

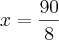





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.