 por FilipeCaceres » Sex Abr 29, 2011 23:17
por FilipeCaceres » Sex Abr 29, 2011 23:17
Ressuscitando um morto,rsrs
Fora de escala.
Vejam o que eu fiz, mas ainda não consegui provar certas coisas, espero que colocando este meu rascunho possa despertar alguma ideia em alguém.
Dados da minha figura.



, pois

e

são minhas bissetrizes externas, logo o ângulo

Minhas bissetrizes externas valem

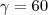
Portanto,
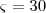

É possível encontrar outros ângulos, mas optei postar apenas estes pois os demais são fáceis de se ver.
Alguém teria alguma dica para provar que

Agradeço desde já.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Sáb Abr 30, 2011 22:47
por FilipeCaceres » Sáb Abr 30, 2011 22:47
Uma forma de mostrar que

seria construir uma cincunferência de raio

desta forma observaríamos que o ponto F perntence a cincunferência, portanto,
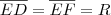
.
Tendo feito isso, temos
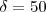
Portanto,

Espero que alguém tenha uma forma mais elegante de resolver esta questão.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3588 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- Trigonometria/Triângulo
 por Pri Ferreira » Qua Mar 21, 2012 14:24
por Pri Ferreira » Qua Mar 21, 2012 14:24
- 1 Respostas
- 2115 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 14:18
Trigonometria
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Qui Set 13, 2012 18:03
- 4 Respostas
- 3289 Exibições
- Última mensagem por Cleyson007

Sex Set 14, 2012 09:36
Trigonometria
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 16:54
- 1 Respostas
- 3178 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:42
Trigonometria
-
- RE: TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 17:08
- 2 Respostas
- 6774 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:31
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 na figura abaixo.
na figura abaixo.


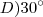


 na figura abaixo.
na figura abaixo.


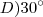




 , pois
, pois  e
e  são minhas bissetrizes externas, logo o ângulo
são minhas bissetrizes externas, logo o ângulo 

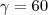
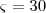



 seria construir uma cincunferência de raio
seria construir uma cincunferência de raio  desta forma observaríamos que o ponto F perntence a cincunferência, portanto,
desta forma observaríamos que o ponto F perntence a cincunferência, portanto, 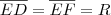 .
.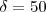



 .
.



