 por Sobreira » Sáb Ago 03, 2013 15:38
por Sobreira » Sáb Ago 03, 2013 15:38
Tenho o desenho abaixo para tentar exemplificar o problema.
O detalhe é o seguinte:
Para determinar o módulo do vetor resultante, através da regra do polígono, eu aplico diretamente a lei dos cossenos:
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 cos 110} Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 cos 110}](/latexrender/pictures/f43650bb8a65473d5fa693bbb2e85596.png)
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (-0,342020)} Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (-0,342020)}](/latexrender/pictures/fb976e317e0f41bf85ac7b9f7d5c7f72.png)
Até aí tudo bem.Mas se eu quero, por exemplo, realizar o exercício pela regra do paralelogramo, no cálculo eu ficarei com cosseno de 70º que é o mesmo de 110º mas negativo.O cosseno de 110º é -0,34 e o cosseno de 70º é 0,34.
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (0,342020)} Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (0,342020)}](/latexrender/pictures/8617085aa439c743b3ffa949c3928a3d.png)
Este sinal de negativo altera completamente o resultado do exercício.
Qual a solução ??
- Anexos
-
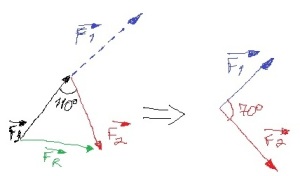
- Sem título.jpg (9.82 KiB) Exibido 1104 vezes
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por mecfael » Dom Ago 18, 2013 22:52
por mecfael » Dom Ago 18, 2013 22:52
Pela regra do paralelogramo na formula fica:
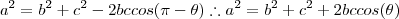
então ai não vai dar erro
-
mecfael
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 17, 2013 23:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Trigonometria] Soma de SENO
por marcelodavid » Ter Jan 03, 2012 20:34
- 7 Respostas
- 5733 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 04, 2012 12:56
Trigonometria
-
- [Trigonometria] soma de cossenos
por blaze » Ter Jun 03, 2014 15:43
- 4 Respostas
- 3429 Exibições
- Última mensagem por blaze

Ter Jun 03, 2014 21:29
Trigonometria
-
- [Trigonometria] Exercicio envolvendo soma de cos.
por combatente20 » Seg Mai 26, 2014 16:56
- 1 Respostas
- 3586 Exibições
- Última mensagem por e8group

Ter Mai 27, 2014 00:46
Trigonometria
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2096 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7363 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 cos 110} Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 cos 110}](/latexrender/pictures/f43650bb8a65473d5fa693bbb2e85596.png)
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (-0,342020)} Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (-0,342020)}](/latexrender/pictures/fb976e317e0f41bf85ac7b9f7d5c7f72.png)
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (0,342020)} Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (0,342020)}](/latexrender/pictures/8617085aa439c743b3ffa949c3928a3d.png)


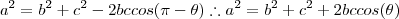 então ai não vai dar erro
então ai não vai dar erro
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.