O detalhe é o seguinte:
Para determinar o módulo do vetor resultante, através da regra do polígono, eu aplico diretamente a lei dos cossenos:
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 cos 110}](/latexrender/pictures/f43650bb8a65473d5fa693bbb2e85596.png "Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 cos 110}")
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (-0,342020)}](/latexrender/pictures/fb976e317e0f41bf85ac7b9f7d5c7f72.png "Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (-0,342020)}")
Até aí tudo bem.Mas se eu quero, por exemplo, realizar o exercício pela regra do paralelogramo, no cálculo eu ficarei com cosseno de 70º que é o mesmo de 110º mas negativo.O cosseno de 110º é -0,34 e o cosseno de 70º é 0,34.
![Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (0,342020)}](/latexrender/pictures/8617085aa439c743b3ffa949c3928a3d.png "Fr=\sqrt[]{{F1}^{2}+{F2}^{2}-2 F1 F2 (0,342020)}")
Este sinal de negativo altera completamente o resultado do exercício.
Qual a solução ??
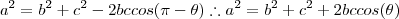então ai não vai dar erro
.
: