sen x= 2-2x+x²
Tentei fazer substituindo sen x por este intervalo:
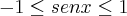
Ai fica:

Não consigo sair dai.A reposta é uma solução

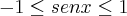





nan_henrique escreveu:Boa Noite, molina
Na apostila está isso mesmo, nenhuma solução.
Mas só não entendi como vc fez o grafico da função do segundo grau e achou o vertice e viu que o ponto era incomum.
Muito Obrigado desde já.

 . Mas o gráfico do
. Mas o gráfico do 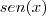 não passa por esse ponto, já que quando
não passa por esse ponto, já que quando  , x vale
, x vale  .
.
 entao não seria uma?
entao não seria uma?
nan_henrique escreveu:Desculpa, mas ainda nao consegui entender.
O vertice da parabola é (1,1), e o senentao não seria uma?
Obrigado
 da parábola significa que quando x é 1, y é 1.
da parábola significa que quando x é 1, y é 1.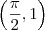 do seno significa que quando x é
do seno significa que quando x é  , y é 1.
, y é 1.





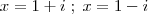


nan_henrique escreveu:Douglasm,
Não entendi como vc resolveu essas inequações.

Douglasm escreveu:nan_henrique escreveu:Douglasm,
Não entendi como vc resolveu essas inequações.
Desculpe Henrique, elas eram desnecessárias.



Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)